Dwusieczna kąta

Co to jest dwusieczna kąta?

Definicja

Dwusieczna kąta jest to półprosta o początku w wierzchołku kąta, która leży na osi symetrii kąta i leży w obszarze tego kąta.

Poniższy rysunek ilustruje dwusieczną kąta wklęsłego i wypukłego.

Dwusieczna kąta dzieli kąt na dwa kąty przystające.

Konstrukcja dwusiecznej kąta

Poniżej przedstawiono sposób w jaki sposób narysować dwusieczną kąta.

Własności dwusiecznej kąta

Twierdzenie

Dwusieczna kąta wypukłego i niepółpełnego jest zbiorem wszystkich punktów leżących w obszarze tego kąta i mających jednakowe odległości od ramion tego kąta.

Pytania

Gdzue wykorzystuje się pojęcie dwusiecznej kąta?

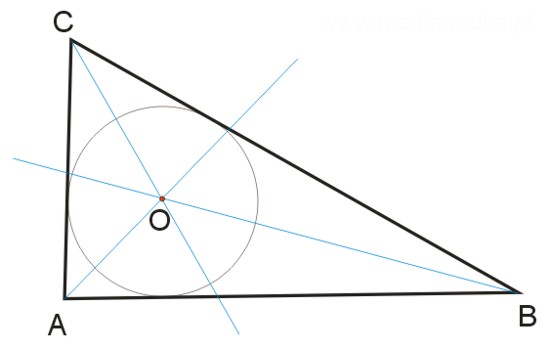
Dwusieczne kątów w trójkacie przecinają się w jednym punkcie, który jest środkiem okręgu wpisanego w ten trójkąt.

okrąg wpisany w trójkąt - konstrukcja

Zadania z rozwiązaniami

Zadanie nr 1.

Skonstruować dwusieczną kąta przedstawionego na rysunku.

dwusieczna kąta

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Znaleźć równanie dwusiecznej kątów wyznaczonych przez proste o równaniach $y=-\frac{3}{4}x+\frac{1}{2}$ i $y=\frac{4}{3}x+\frac{5}{3}$ .

Pokaż rozwiązanie zadania.

Zadanie nr 3 — maturalne.

Dwusieczne czworokąta ABCD wpisanego w okrąg przecinają się w czterech różnych punktach:, Q, R, S (zobacz rysunek)
rysunek do zanaia 9, matura 2015

Wykaż, że na czworokącie PQRS można opisać okrąg.

Pokaż rozwiązanie zadania.

Inne zagadnienia z tej lekcji

Przekształcenie geometryczne

Definicja przekształcenia geometrycznego, izometrycznego, tożsamościowego.

Symetria osiowa

Symetria osiowa względem prostej a jest to nietożsamościowa izometria płaszczyzny, w której każdy punkt prostej a jest punktem stałym.

Symetria środkowa

Co to jest symetria środkowa względem punktu i środek symetrii figury?

Symetria z poślizgiem

Symetria z poślizgiem to złożenie translacji i symetrii osiowej względem prostej równoległej do wektora translacji.

Symetralna odcinka

Symetralna odcinka jest to oś symetrii tego odcinka prostopadła do niego.