Energia potencjalna w polu grawitacyjnym

Siła grawitacji jest to siła zachowawcza, to znaczy, że praca przez nią wykonana przy przemieszczaniu ciała w polu grawitacyjnym nie zależy od drogi i toru ruchu, a jedynie od położenia początkowego i końcowego ciała w polu grawitacyjnym. Stwierdzenie to obowiązuje dla pół niezmiennych (stacjonarnych).

Praca w polu grawitacyjnym

Praca wykonana przez siłę zewnętrzną, równoważącą siłę grawitacji przy przesunięciu ciała o masie m z punktu A do punktu B w polu grawitacyjnym źródła pola o masie M jest równa:

$W_{z,A\to B}=GMm(\frac{1}{r_A}-\frac{1}{r_B})$ .

Natomiast praca sił pola grawitacyjnego w powyższych warunkach jest równa:

$W_{g,A\to B}=-GMm(\frac{1}{r_A}-\frac{1}{r_B})$

Z powyższych wzorów wynika prosty wniosek:

Praca w polu grawitacyjnym po drodze zamkniętej jest równa zeru.

Ponieważ zmienia się położenie ciała o masie m w polu grawitacyjnym ciała o masie M, energia potencjalna również się zmienia i jest równa pracy, jaka wykona siła zewnętrzna, równoważąca w każdym punkcie siłę grawitacji.

$\Delta E_p=GMm(\frac{1}{r_A}-\frac{1}{r_B})$

Z powyższego wzoru wynika wniosek, że energia potencjalna rośnie, gdy ciało próbne oddala się od źródła pola, a maleje, gdy zbliża się do źródła.

Jak policzyć energię potencjalną w danym punkcie? Trzeba przyjąć jakiś punkt odniesienia. Przyjęło się, że wartość energii potencjalnej w nieskończoności jest równa zeru. Konsekwencją powyższych dwóch wniosków jest to, że energia potencjalna może być tylko ujemna lub równa zero w nieskończoności. Ponieważ r_B→∞, to 1/r_B→0 i:

$E_p_A=-\frac{GMm}{r_A}$

Potencjał pola grawitacyjnego

Aby znaleźć wielkość fizyczną, która opisze skalarnie pole grawitacyjne, wystarczy uniezależnić powyższy wzór od masy ciała próbnego. Wielkość fizyczną taką nazywamy potencjałem pola.

Potencjał pola grawitacyjnego jest to iloraz energii potencjalnej ciała w tym polu do masy tego ciała. Potencjał oznaczamy symbolem V.

$V=\frac{E_p}{m}$

Dla pola centralnego i podstawieniu odpowiednich wzorów otrzymamy:

$V=-\frac{GM}{r}$

Dla pola jednorodnego:

$V=-\frac{E_p}{m}=\frac{mgh}{m}=gh$

Inne zagadnienia z tej lekcji

Prawo powszechnego ciążenia

Dwa punkty materialne przyciągają się wzajemnie siłą proporcjonalną do iloczynu tych mas i odwrotnie proporcjonalną do kwadratu odległości między tymi punktami.

Przyspieszenie ziemskie

Przyspieszenie ziemskie jest to przyspieszenie, jakie uzyskują ciała spadające na powierzchnię Ziemi. Oznaczamy je literą g. Jest ono równe w przybliżeniu 9,81 m/s2.

Pole grawitacyjne

Jeżeli w absolutnej próżni umieścimy ciało obdarzone masą M, to w przestrzeń wokół tego ciała zostanie zmieniona. wielkością, która opisuje tę przestrzeń jest natężenie pola grawitacyjnego.

Pierwsza prędkość kosmiczna

Aby ciało to poruszało się po orbicie kołowej wokół Ziemi należy mu nadać tak zwaną pierwszą prędkość kosmiczną. Co to jest orbita geostacjonarna?

Druga prędkość kosmiczna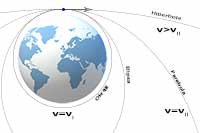

Druga prędkość kosmiczna jest to najmniejsza z możliwych prędkości, jaką należy nadać ciału przy powierzchni Ziemi, aby mogło oddalić się do nieskończoności. Jest to tak zwana prędkość ucieczki.