Okrąg
Co to jest okrąg?
Definicja
Okrąg o środku \(S\) i promieniu \(r\) jest to zbiór punktów płaszczyzny, których odległości od punktu \(S\) są równe liczbie dodatniej \(r\).
Okrąg o środku \(S\) i promieniu \(r\) oznaczamy następująco: \(o(S,r)\).
Promień jest więc odcinkiem \(\overline{r}\) o długości \(r\). Należy pamiętać, że zarówno środek okręgu \(S\), jak i promień okręgu \(r\) nie należy do okręgu.
Równanie okręgu
W odrębnym artykule piszemy o tym, jak można opisać okrąg w układzie współrzędnych. Podajemy tam równanie okręgu. Jest to tak zwane równanie kanoniczne okręgu.
gdzie \(r>0\) jest promieniem okręgu, a \(S(p,q)\) jest jego środkiem.
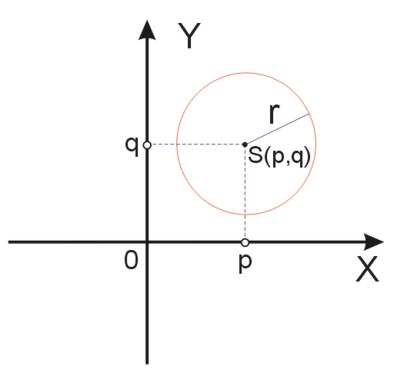
Więcej na ten temat znajdziesz tutaj.
Koło
Co to jest koło i czym się różni od okręgu?
Definicja
Koło o środku \(S\) i promieniu \(r\) jest to zbiór punktów płaszczyzny, których odległości od punktu \(S\) są mniejsze lub równe liczbie dodatniej \(r\).
Koło o środku \(S\) i promieniu \(r\) oznaczamy następująco: \(k(S,r)\).
Promień jest odcinkiem \(\overline{r}\) o długości \(r\). W przypadku koła środek okręgu \(S\) jak i promień okręgu \(r\) należy do okręgu.
Warto też zauważyć, że okrąg stanowi brzeg koła.
Cięciwa okręgu
Z pojęciem okręgu i koła wiążą się inne pojęcia matematyczne. Oto niektóre z nich:
Cięciwa okręgu jest to odcinek łączący dwa różne punkty okręgu.
Średnica okręgu
Średnica okręgu jest to cięciwa przechodząca przez środek okręgu.
Z powyższych definicji możemy wywnioskować następujące wnioski:
- Długość średnicy jest równa podwojonej długości promienia okręgu, czyli \(2r\).
- Średnica jest najdłuższą cięciwą okręgu.
Sieczna i odcinek koła
Sieczna okręgu (lub koła) jest to prosta wyznaczona przez dwa różne punkty okręgu (brzegu koła).
Odcinek koła jest to część koła po jednej stronie siecznej wraz z cięciwą należącą do tej siecznej. Sieczna wyznacza dwa odcinki koła, a cięciwa należy zarówno do jednego, jak i do drugiego odcinka koła.
Pole koła i długość okręgu
Pole koła i obwód okręgu omawiamy w osobnym artykule tutaj.
Twierdzenia o okręgu
Twierdzenie 1
Kąt ostry między cięciwą i styczna, która przechodzi przez koniec cięciwy, jest równy połowie kąta środkowego odpowiadającego cięciwie.
Twierdzenie 2
Wszystkie kąty wpisane w dany okrąg i oparte na tym samym łuku są równe i równe połowie kąta środkowego opartego na tym samym łuku.
Twierdzenie 3
Kąt wpisany w półkole oparty na średnicy jest kątem prostym.
Twierdzenie 4
Odcinek prostopadłej opuszczonej z dowolnego punktu okręgu na średnicę jest średnią geometryczną odcinków, na które ta prostopadła dzieli średnicę.
\(h=\sqrt{xy}\)
Twierdzenie 5
Odcinki leżące na dwóch stycznych do okręgu, poprowadzonych z dowolnego punktu zewnętrznego, wyznaczone przez ten punkt oraz punkty styczności są równe.
Okrąg opisany na wielokącie
Okrąg opisany na wielokącie jest to okrąg, do którego należą wszystkie wierzchołki tego wielokąta. Można też powiedzieć, że wielokąt jest wpisany w okrąg.
Nie na każdym wielokącie można opisać okrąg. Okrąg można opisać na takim wielokącie, którego symetralne boków przecinają się w jednym punkcie, który stanowi właśnie środek tego okręgu.
Okrąg można opisać na każdym trójkącie. Więcej na ten temat znajdziesz tutaj.
Okrąg można opisać na czworokącie wtedy i tylko wtedy, gdy sumy miar przeciwległych kątów są równe.
Trapez wpisany w okrąg
Na każdym trapezie równoramiennym można opisać okrąg. Aby wyznaczyć środek okręgu opisanego na trapezie, należy wyznaczyć punkt przecięcia się symetralnych dwóch boków trapezu (przynajmniej jednego ramienia).
Kwadrat i prostokąt wpisany w okrąg
Każdy kwadrat i prostokąt posiada okrąg opisany. Środek okręgu opisanego leży na przecięciu przekątnych kwadratu lub prostokąta.
Okrąg wpisany w wielokąt
Okrąg wpisany w wielokąt jest to okrąg, do którego są styczne wszystkie boki danego wielokąta. Mówimy też, że wielokąt jest opisany na okręgu.
Środek okręgu wpisanego w wielokąt leży na przecięciu dwusiecznych kątów tego wielokąta.
W każdy trójkąt można wpisać okrąg. Więcej na ten temat znajdziesz tutaj.
W czworokąt można wpisać okrąg, gdy jest on wypukły i sumy długości jego przeciwległych boków są równe.
Pytania
Czym się różni koło od okręgu?
Okrąg jest brzegiem koła. Do koła zatem należą także punkty wewnątrz okręgu. Czasem błędnie się sądzi, że środek należy do okręgu. Środek należy do koła, do okręgu już nie.
Jak wyznaczyć środek okręgu?
Wystarczy wybrać dowolne dwie cięciwy okręgu i znaleźć ich symetralne. Punkt przecięcia się tych symetralnych jest środkiem okręgu.
Czy w każdy kwadrat można wpisać okrąg?
Tak. Jego środek leży na przecięciu przekątnych kwadratu.
Czy w prostokąt można wpisać okrąg?
Nie.
Czy w trapez można wpisać okrąg?
Tak, ale tylko w taki, którego sumy długości jego przeciwległych boków są równe.
Co to jest okrąg wielki sfery?
Jest to okrąg, który powstał przez przekrój sfery płaszczyzną przechodzącą przez środek tej sfery.
Jak sprawdzić, czy podane równanie jest równaniem okręgu?
Problem ten omawiamy tutaj.
Jak opisać okrąg na trójkącie?
Problem ten omawiamy tutaj.
Zadania z rozwiązaniami
Zadanie nr 1.
Przez punkty \(A, B\) na okręgu o promieniu \(r=2,5\) poprowadzono średnicę. Punkt \(D\) leży na okręgu tak, że \(|BD|=4\). Oblicz odległość \(|AD|\).
Zadanie nr 2.
Na średnicy okręgu o promieniu długości 6 obrano punkt \(A\) w taki sposób, że punkt ten dzieli promień okręgu w stosunku 1 do 2 (krótszy odcinek znajduje się bliżej okręgu). Obliczyć obwód trójkątów wyznaczonych przez średnicę i odcinek prostopadłej przechodzący przez punkt \(A\).
Zadanie nr 4 — maturalne.
Punkty \(ABCD\) leżą na okręgu o środku \(S\) (zobacz rysunek). Miara kąta \(BDC\) jest równa:
A. 91°
B. 72,5°
C. 18°
D. 32°
Zadanie nr 5 — maturalne.
Miara kąta wpisanego w okrąg jest o \(20°\) mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa:
A. \(5°\)
B. \(10°\)
C. \(20°\)
D. \(30°\)
Zadanie nr 6 — maturalne.
Środek \(S\) okręgu opisanego na trójkącie równoramiennym \(ABC\), o ramionach \(AC\) i \(BC\), leży wewnątrz tego trójkąta (zobacz rysunek).
Wykaż, że miara kąta wypukłego \(ASB\) jest cztery razy większa od miary kąta wypukłego \(SBC\).
Zadanie nr 7 — maturalne.
Na okręgu o środku w punkcie \(O\) leży punkt \(C\) (zobacz rysunek). Odcinek \(AB\) jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy \(\alpha\) ma miarę:
A. \(m=116°
B. \(m=114°
C. \(m=112°
D. \(m=110°
Zadanie nr 8 — maturalne.
Dany jest okrąg o środku \(S\). Punkty \(K, L\) i \(M\) leżą na tym okręgu. Na łuku \(KL\) tego okręgu są oparte kąty \(KSL\) i \(KML\) (zobacz rysunek), których miary \(\alpha\) i \(\beta\), spełniają warunek \(\alpha +\beta=111°\). Wynika stąd, że
A. \(\alpha=74°\)
B. \(\alpha=76°\)
C. \(\alpha=70°\)
D. \(\alpha=72°\)
Zadanie nr 9 — maturalne.
Okręgi o środkach odpowiednio \(A\) i \(B\) są styczne zewnętrznie i każdy z nich jest styczny do obu ramion danego kąta prostego (zobacz rysunek). Promień okręgu o środku \(A\) jest równy 2.
Uzasadnij, że promień okręgu o środku \(B\) jest mniejszy od \(\sqrt{2}-1\).
Zadanie nr 10 — maturalne.
Trójkąt \(ABC\) jest ostrokątny oraz \(|AC|>|BC|\). Dwusieczna \(d_C\) kąta \(ACB\) przecina bok \(AB\) w punkcie \(K\). Punkt \(L\) jest obrazem punktu \(K\) w symetrii osiowej względem dwusiecznej \(d_A\) kąta \(BAC\), punkt \(M\) jest obrazem punktu \(L\) w symetrii osiowej względem dwusiecznej \(d_C\) kąta \(ACB\), a punkt \(N\) jest obrazem punktu \(M\) w symetrii osiowej względem dwusiecznej \(d_B\) kąta \(ABC\) (zobacz rysunek).
Udowodnij, że na czworokącie \(KNML\) można opisać okrąg.
Zadanie nr 11 — maturalne.
Punkty \(D\) i \(E\) leżą na okręgu opisanym na trójkącie równobocznym \(ABC\) (zobacz rysunek). Odcinek \(CD\) jest średnicą tego okręgu. Kąt wpisany \(DEB\) ma miarę \(\alpha\).
A. \(\alpha=30°\)
B. \(\alpha<30°\)
C. \(\alpha>45°\)
D. \(\alpha=45°\)
Zadanie nr 12 — maturalne.
Punkty \(A, B, C, D\) leżą na okręgu o środku w punkcie \(O\). Kąt środkowy \(DOC\) ma miarę 118° (zobacz rysunek).
Miara kąta ABC jest równa
A. 59°
B. 48°
C. 62°
D. 31°
Zadanie nr 13 — maturalne.
Punkty A, B, C leżą na okręgu o środku S. Punkt D jest punktem przecięcia cięciwy AC i średnicy okręgu poprowadzonej z punktu B. Miara kąta BSC jest równa α, a miara kąta ADB jest równa γ (zobacz rysunek).
Wtedy kąt ABD ma miarę
A. \(\frac{\alpha}{2}+\gamma−180°\)
B. \(180°-\frac{\alpha}{2}-\gamma\)
C. \(180°-\alpha-\gamma\)
D. \(\alpha+\gamma−180°\)
Zadanie nr 14 — maturalne.
Punkty \(A, B, C\) leżą na okręgu o środku w punkcie \(O\). Kąt \(ACO\) ma miarę 70° (zobacz rysunek). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Miara kąta ostrego \(ABC\) jest równa:
A. \(10°\)
B. \(20°\)
C. \(35°\)
D. \(40°\)
Wybrane karty pracy
Okrąg i koło
Powiązane materiały
Liczba pi
Pole koła i długość okręgu
Wzajemne położenie okręgów
Pierścień kołowy
Pole wycinka kołowego
Równanie okręgu
Dlaczego garnki są okrągłe?
Okręgi i koła
Okrąg i koło — quiz© medianauka.pl, 2010-10-28, A-994
Data aktualizacji artykułu: 2023-06-12