Pierwsza prędkość kosmiczna

Zastanawiałeś się kiedyś w jaki sposób satelity poruszają się mimo, że nie posiadają silników? Spójrz na poniższą animację.

Satelita porusza się po okręgu ze stałą szybkością, a rolę siły dośrodkowej pełni siła grawitacji. Możemy więc napisać, że:

$\frac{mv^2}{r}=G\frac{mM}{r^2}/\cdot\frac{r}{m}\\v^2=\frac{GM}{r}$

Pierwiastkując obie strony równania otrzymujemy wzór na prędkość, jaką należy nadać ciału stycznie do krzywizny Ziemi, aby ciało to poruszało się po orbicie kołowej wokół Ziemi. Jest to tak zwana pierwsza prędkość kosmiczna.

$v_{I}=\sqrt{\frac{GM}{r}}$

W przypadku Ziemi możemy podstawić następujące wartości do powyższego wzoru:

r=R_Z=6,37·10⁶ m,

M=M_z=6·10²⁴ kg,

$G=6,67\cdot 10^{-11}\quad\frac{Nm^2}{kg^2}$ ,

otrzymując pierwszą prędkość kosmiczną ziemską, tuż przy powierzchni Ziemi.

v_IZ≈7,9 km/s

W rzeczywistości opór powietrza, który tu został pominięty szybko doprowadziłby do spadku satelity na powierzchnię Ziemi lub w wyniku tarcia z powietrzem satelita spaliłby się w atmosferze. Satelity Ziemi latają więc na wysokości około 500 km nad jej powierzchnią.

Jak widzisz, satelita w rzeczywistości cały czas "spada" na powierzchnię Ziemi. Nie potrzebuje więc żadnego napędu, aby utrzymywać się na torze ruchu wokół Ziemi.

Orbita geostacjonarna

Jeżeli okres obiegu satelity wokół ciała jest równy okresowi obrotu tego ciała, to mówimy, że satelita ten znajduje się na orbicie geostacjonarnej. Satelita na takiej orbicie znajduje się stale nad jednym punktem na powierzchni Ziemi. Wydaje się , że w ogóle się nie porusza. Ruch odbywa się w płaszczyźnie równika z zachodu na wschód w odległości 42 160 km od środka Ziemi.

Inne zagadnienia z tej lekcji

Prawo powszechnego ciążenia

Dwa punkty materialne przyciągają się wzajemnie siłą proporcjonalną do iloczynu tych mas i odwrotnie proporcjonalną do kwadratu odległości między tymi punktami.

Przyspieszenie ziemskie

Przyspieszenie ziemskie jest to przyspieszenie, jakie uzyskują ciała spadające na powierzchnię Ziemi. Oznaczamy je literą g. Jest ono równe w przybliżeniu 9,81 m/s2.

Pole grawitacyjne

Jeżeli w absolutnej próżni umieścimy ciało obdarzone masą M, to w przestrzeń wokół tego ciała zostanie zmieniona. wielkością, która opisuje tę przestrzeń jest natężenie pola grawitacyjnego.

Energia potencjalna w polu grawitacyjnym

Siła grawitacji jest to siła zachowawcza, to znaczy, że praca przez nią wykonana przy przemieszczaniu ciała w polu grawitacyjnym nie zależy od drogi i toru ruchu, a jedynie od położenia początkowego i końcowego ciała w polu grawitacyjnym ...

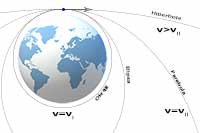Druga prędkość kosmiczna

Druga prędkość kosmiczna jest to najmniejsza z możliwych prędkości, jaką należy nadać ciału przy powierzchni Ziemi, aby mogło oddalić się do nieskończoności. Jest to tak zwana prędkość ucieczki.

Winda kosmiczna - czy da się ją zbudować?

Czy z satelity krążącego po orbicie geostacjonarnej dałoby się spuścić linę i transportować nią w kosmos przedmioty czy ludzi? Czy można w ten sposób zbudować windę kosmiczną?