Pole rombu

Jak obliczyć pole rombu? Zarówno wzory na pole, jak i obwód rombu wynikają bezpośrednio ze wzorów na pole i obwód równoległoboku. W tym przypadku długości wszystkich boków są takie same, natomiast kąt przecięcia się przekątnych rombu ma miarę 90°.

Podstawowy wzór na pole powierzchni rombu jest następujący:

Pole rombu wyraża się wzorem:

\(P=ah\)

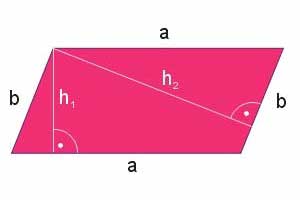
Wielkość \(a\) jest długością boku rombu, a \(h\) jego wysokością (patrz rysunek).

pole rombu

Przykłady

Obliczyć pole rombu przedstawionego na rysunku.

Rozwiązanie: Dana jest długość boku \(a=3,7\) oraz wysokość \(h=3,5\). Stosujemy więc bezpośrednio wzór na pole rombu:

\(P=3,5\cdot 3,7=12,95\)

Inne wzory na pole rombu

Jeżeli są dane przekątne rombu. Pole powierzchni tej figury geometrycznej możemy obliczyć z następującego wzoru:

Pole rombu z przekątnych \(d_1, d_2\) wyraża się wzorem:

\(P=\frac{1}{2}d_1d_2\)

pole rombu - zadanie

Wzór na pole rombu jest następujący:

\(P=a^2\cdot \sin{\alpha}\)

Wielkość \(a\) jest długością boku, a \(\alpha\) jest kątem między dwoma bokami rombu (patrz na rysunek).

romb

Pole rombu wyznaczonego przez dwa niezerowe wektory zaczepione we wspólnym początku jest równe modułowi wyznacznika \(W\) tych wektorów.

\(W=\begin{vmatrix} a_x&a_y\\b_x&b_y \end{vmatrix}=a_xb_y-a_yb_x\)

\(P=|W|\)

pole rombu - wektory

Obwód rombu

Wzór na obwód rombu o boku długości \(a\) jest następujący:

\(L=4a\)

Zadania z rozwiązaniami

Zadanie nr 1.

Przekątna kwadratu o boku 1 oraz połowa drugiej przekątnej kwadratu stanowią przekątne rombu. Oblicz jego pole i obwód.

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Oblicz pole rombu \(ABCD\), jeżeli wiadomo, że \(A=(2,0), B=(3,2), C=(2,4), D=(1,2)\).

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Dany jest romb o boku \(a=\sqrt{2}\). Kąt wewnętrzny ma miarę 60°. Obliczyć pole powierzchni tego rombu.

Pokaż rozwiązanie zadania.

Zadanie nr 4.

Wysokość rombu o polu 3 ma wartość \(\frac{3}{2}\). Oblicz obwód tego rombu.

Pokaż rozwiązanie zadania.

Zadanie nr 5 — maturalne.

Pole rombu o obwodzie 8 jest równe 1. Kąt ostry tego rombu ma miarę \(\alpha\). Wtedy:

A. \(14°<\alpha< 15°\)

B. \(29°<\alpha< 30°\)

C. \(60°<\alpha< 61°\)

D. \(75°<\alpha< 76°\)

Pokaż rozwiązanie zadania.

Zadanie nr 6 — maturalne.

Dany jest kwadrat \(ABCD\). Przekątne \(AC\) i \(BD\) przecinają się w punkcie \(E\). Punkty \(K\) i \(M\) są środkami odcinków – odpowiednio – \(AE\) i \(EC\). Punkty \(L\) i \(N\) leżą na przekątnej \(BD\) tak, że \(|BL|=\frac{1}{3}|BE|\) i \(|DN|=\frac{1}{3}|DE|\) (zobacz rysunek). Wykaż, że stosunek pola czworokąta \(KLMN\) do pola kwadratu \(ABCD\) jest równy 1:3.

Zadanie maturalne 28 2015