Pole trapezu

Jak obliczyć pole trapezu? Jaki jest wzór na pole trapezu?

Twierdzenie

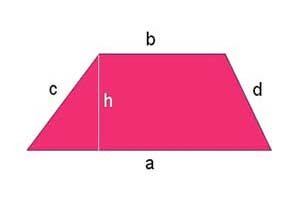
Pole trapezu wyraża się wzorem:

$P=\frac{1}{2}(a+b)\cdot h$

gdzie a, b są długościami podstaw trapezu, a h jego wysokością.

Przykład

Obliczyć pole trapezu o podstawach długości 10 i 5 oraz wysokości h=2.

Rozwiązanie: Dane są podstawy a=5 oraz b=10 oraz wysokość h=2. Stosujemy więc bezpośrednio wzór na pole trapezu:

$P=\frac{1}{2}(a+b)\cdot h=\frac{1}{2}(5+10)\cdot 2=15$

Inne wzory na pole powierzchni trapezu

Gdy dane są przekątne trapezu d₁ i d₂ oraz kąt φ, jaki tworzą te przekątne, to pole trapezu obliczymy ze wzoru:

P=1/2·d₁·d₂·sinφ

Gdy dane są długości podstaw trapezu a i b, długość ramienia c oraz kąt β, jaki tworzy to ramię z podstawą, to pole trapezu obliczymy ze wzoru:

P=1/2·(a+b)·c·sinβ

Obwód trapezu

Twierdzenie

Obwód trapezu wyraża się wzorem:

gdzie a, b, c, d są długościami boków trapezu.

Pytania

Jak obliczyć pole trapezu gdy nie ma podanej wysokości?

W przypadku, gdy dane są długości wszystkich boków, a trapez jest równoramienny, to wysokość trapezu można wyznaczyć na podstawie twierdzenia Pitagorasa. Ramię, szukana wysokość i część odcinka podstawy tworzą trójkąt prostokątny. Ten krótki odcinek podstawy obliczamy, odejmując od długości dłuższej podstawy długość krótszej podstawy i dzielimy przez 2.

W innych przypadkach na ogół korzystamy z funkcji trygonometrycznych lub wzorów wymienionych wyżej.

Zadania z rozwiązaniami

Zadania związane z tematem:
Pole i obwód trapezu

Zadanie - własności trójkąta, obwód trapezu
Dany jest trójkąt ABC o bokach długości: |AB|=6, |BC|=4, |AC|=5. Punkt M jest środkiem boku AC, punkt N - środkiem boku BC. Obliczyć obwód trapezu ABNM.

Pokaż rozwiązanie zadania

Zadanie - pole powierzchni trapezu
Oblicz pole trapezu równoramiennego, którego wysokość ma długość 2, krótsza podstawa 4, a ramię ma długość 3.

Pokaż rozwiązanie zadania

Inne zagadnienia z tej lekcji

Prostokąt

Prostokąt jest to równoległobok, który ma wszystkie kąty proste.

Pole i obwód prostokąta

Pole prostokąta wyraża się wzorem: P=ab. Obwód prostokąta wyraża się wzorem: L=2a+2b.

Kwadrat

Kwadrat jest to równoległobok, który ma wszystkie kąty proste i wszystkie boki równe.

Trapez

Trapez jest to czworokąt, który ma co najmniej jedną parę boków równoległych.

Równoległobok

Równoległobok jest to czworokąt, która ma dwie pary boków równoległych.

Pole równoległoboku

Pole równoległoboku wyraża się wzorem: P=ah1=bh2, gdzie a,b to długości boków, a h1,h2 to wysokości.

Romb

Romb jest to równoległobok, który ma wszystkie boki równe. W rombie przekątne są prostopadłe do siebie.

Pole rombu

Wzory na pole i obwód rombu wynikają bezpośrednio ze wzorów na pole i obwód równoległoboku.

Deltoid

Deltoid jest to czworokąt, którego dwa kolejne boki są równe i dwa kolejne boki są równe między sobą, ale różne od poprzednich.

Pole deltoidu

Pole deltoidu wyraża się wzorem: P=1/2d1d2, gdzie d1, d2 są długościami przekątnych.

Test wiedzy

Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.

Powiązane quizy

Pole trapezu

Szkoła podstawowa
Klasa 5
Liczba pytań: 8

Pole trapezu

karta081.pdf
Szkoła podstawowa
Klasa 5