Proste równoległe

Definicja

Proste a i b są równoległe jeżeli nie mają punktu wspólnego lub pokrywają się. Dla oznaczenia równoległości prostych używamy zapisu: a||b.

Analityczne podejście do równoległości prostych znajdziesz w artykule: Wzajemne położenie prostych na płaszczyźnie.

Konstrukcja prostej równoległej
(kreślenie prostej równoległej)

Poniżej został zamieszczony krótki film, który pokazuje jak skonstruować prostą równoległą do danej prostej przechodzącej przez punkt A.

Dwie proste na płaszczyźnie są równoległe jeżeli mają równe współczynniki kierunkowe a.

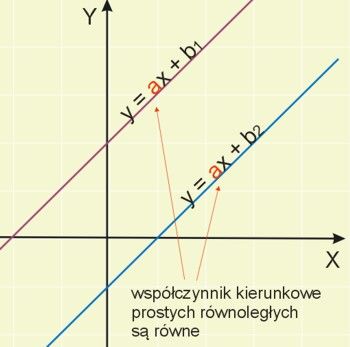
proste równoległe

Przykład

Dwie proste y=2x+1 i y=2x-20 są równoległe, ponieważ mają taki sam współczynnik kierunkowy prostej a=2.

Zadanie nr 1 — maturalne.

Proste o równaniach y=(m+2)x+3 oraz y=(2m−1)x−3 są równoległe, gdy

Proste prostopadłe

Prostą a nazywamy prostopadłą do prostej b, jeżeli prosta b jest osią symetrii prostej a i jest od niej różna.

Pole figury

Pole figury płaskiej jest to funkcja, która każdej figurze geometrycznej płaskiej przyporządkowuje liczbę nieujemną w taki sposób, że ...

Test wiedzy

Sprawdź swoje umiejętności z materiału zawartego w tej lekcji.