Przesunięcie wykresu funkcji

Jeżeli punkt $A$ o współrzędnych $(x, y)$ przesuniemy w układzie współrzędnych o wektor $\vec{v} = [p, q]$ , to otrzymamy punkt $A^{'}$ o współrzędnych $(x + p, x + q)$ .
przesunięcie punktu o wektor w układzie współrzędnych
Ponieważ wykres funkcji (oznaczmy go literą $W$ ) jest figurą geometryczną, więc przesunięcie całego wykresu polega na przesunięciu wszystkich punktów wykresu o ten sam wektor przesunięcia.

Wiemy, że każdy punkt wykresu $W$ spełnia zależność $y = f (x)$ . Jaki będzie zatem wzór funkcji wykresu $W^{'}$ powstałego z przesunięcia wykresu $W$ o wektor $\vec{v} = [p, q]$ ?

Przesunięcie wykresu funkcji o wektor

Jeżeli współrzędne punktów należących do wykresu $W^{'}$ mają postać $(x, y)$ , to współrzędne punktów wykresu W są postaci $(x - p, y - q)$ . Podstawiamy więc współrzędne do wzoru funkcji i otrzymujemy: $y - q = f (x - p)$ .

y = f (x - p) + q

Otrzymaliśmy w ten sposób wykres funkcji $y = f (x)$ przesunięty w układzie współrzędnych o wektor $\vec{v} = [p, q]$ .

Przykład

Naszkicujmy wykres funkcji $y = x^{2} - 2 x + 3$ , korzystając z informacji zawartych wyżej.

Aby to uczynić, musimy przekształcić nieco wzór funkcji (doprowadzić do właściwej postaci):

$y = (x^{2} - 2 x + 1) + 2$

$y = (x - 1)^{2} + 2$

Zatem musimy przesunąć wykres funkcji $y = x^{2}$ o wektor $\vec{v} = [1, 2]$ .

przesunięcie wykresu w układzie współrzędnych

Przesuwanie wykresów funkcji w układzie współrzędnych ma duże znaczenie praktyczne. Możemy szybko naszkicować wiele wykresów funkcji, znając jedynie wykresy funkcji elementarnych i powyższą zasadę znajdowania wektora przesunięcia. Poniżej jeszcze kilka przykładów stosowania tej zasady.

Przykłady

Aby naszkicować wykres funkcji $y = \frac{1}{x + 12} + 7$ , wystarczy wykres funkcji $y = \frac{1}{x}$ przesunąć o wektor $\vec{v} = [- 12, 7]$ .
Aby naszkicować wykres funkcji $y = - 1 + \log (x - 8)$ , wystarczy wykres funkcji $y = \log x$ przesunąć o wektor $\vec{v} = [8, - 1]$ .
Aby naszkicować wykres funkcji $y = \cos (x + \frac{π}{6})$ , wystarczy wykres funkcji $y = \cos x$ przesunąć o wektor $\vec{v} = [\frac{π}{6}, 0]$ .
Aby naszkicować wykres funkcji $y = \sqrt{x + 5} - 5$ , wystarczy wykres funkcji $y = \sqrt{x}$ przesunąć o wektor $\vec{v} = [- 5, - 5]$ .

Warto poćwiczyć przesuwanie wykresu funkcji na niżej opublikowanych zadaniach.

Przesunięcie wykresu funkcji wzdłuż osi OX

y = f (x - p)

Otrzymaliśmy w ten sposób wykres funkcji $y = f (x)$ przesunięty w układzie współrzędnych o wektor $\vec{v} = [p, 0]$ .

Przesunięcie wykresu funkcji wzdłuż osi OY

y = f (x) + q

Otrzymaliśmy w ten sposób wykres funkcji $y = f (x)$ przesunięty w układzie współrzędnych o wektor $\vec{v} = [0, q]$ .

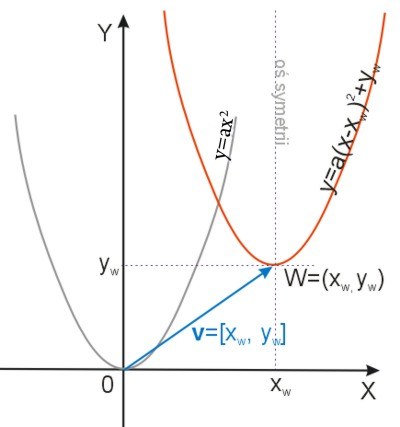
Przesunięcie wykresu funkcji kwadratowej

Wykres funkcji: $y = a x^{2} + b x + c = a (x + \frac{b}{2 a})^{2} - \frac{Δ}{4 a} = a (x - x_{w})^{2} + y_{w}$ jest parabolą, która powstaje w wyniku przesunięcia wykresu funkcji $y = a x^{2}$ o wektor $\vec{v} = [x_{w}, y_{w}]$ , przy czym $x_{w} = - \frac{b}{2 a}, y_{w} = - \frac{Δ}{4 a}$

W przypadku dodatniego współczynnika $a$ mamy:

Wykres funkcji kwadratowej

Zadania z rozwiązaniami

Zadanie nr 1.

Sporządzić wykres funkcji $y = (\frac{1}{2})^{x - 5}$ .

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Sporządzić wykres funkcji $y = (\sqrt{3})^{2 x + 6} + 1$ .

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Naszkicować wykres funkcji $y = \log_{\frac{1}{3}} (x - 3) + 1$ .

Pokaż rozwiązanie zadania.

Zadanie nr 4.

Naszkicować wykres funkcji $y = \log_{2} 4 x$ .

Pokaż rozwiązanie zadania.

Zadanie nr 5.

Naszkicować wykres funkcji $y = \log_{\frac{1}{2}} (\sqrt{2} x + 2 \sqrt{2}) + 1$ .

Pokaż rozwiązanie zadania.

Zadanie nr 6.

Sporządzić wykres funkcji $f (x) = \frac{1}{| x + 2 |} - 3$ .

Pokaż rozwiązanie zadania.

Zadanie nr 7.

Sporządzić wykres funkcji $y = \frac{x - 3}{x - 4}$ .

Pokaż rozwiązanie zadania.

Zadanie nr 8.

Sporządzić wykres funkcji $y = \frac{- 4 x + 7}{2 x - 2}$ .

Pokaż rozwiązanie zadania.

Zadanie nr 9 — maturalne.

Na rysunku przedstawiono fragment wykresu funkcji $f$ , który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem $y = \frac{1}{x}$ dla każdej liczby rzeczywistej $x \neq 0$ .