Równanie okręgu

Równanie okręgu jest szczególnym przypadkiem równania drugiego stopnia z dwiema niewiadomymi. Zanim poznamy wzór na równanie okręgu, zaczniemy od omówienia równania drugiego stopnia z dwiema niewiadomymi.

Równanie drugiego stopnia z dwiema niewiadomymi

Równanie w postaci:

a x^{2} + b y^{2} + c x y + d x + e y + f = 0

gdzie zachodzi co najmniej jedna z zależności: $a \neq 0, b \neq 0, c \neq 0$ , natomiast $d, e, f$ — są dowolnymi liczbami rzeczywistymi, nazywamy równaniem drugiego stopnia z dwiema niewiadomymi.

Przykłady

Kilka przykładów takich równań:

$- x^{2} - 2 y^{2} + 34 y - 5 = 0$
$x y + 1 = 0$
$x^{2} + y^{2} = 0$

Rozwiązanie równania drugiego stopnia z dwiema niewiadomymi polega na podaniu zbioru par liczb, które spełniają dane równanie. Przedstawiamy zwykle obraz geometryczny zbioru rozwiązań takiego równania poprzez sporządzenie wykresu takiego równania.

Wykresem takiego równania może być okrąg, elipsa, parabola, hiperbola. Równanie może też nie mieć rozwiązania lub może spełniać je para liczb.

Równanie kanoniczne okręgu

Szczególnym przypadkiem równania drugiego stopnia z dwiema niewiadomymi jest równanie kanoniczne okręgu.

(x - p)^{2} + (y - q)^{2} = r^{2}

gdzie $r > 0$ jest promieniem okręgu, a $S (p, q)$ jest jego środkiem.

równanie okręgu

Przykłady

Znajdziemy dla przykładu zbiór rozwiązań równania $x^{2} + y^{2} - 6 x - 2 y + 6 = 0$ .

Ponieważ w równaniu nie ma wyrazu $x y$ , a obie niewiadome występują w drugiej potędze, prawdopodobnie wykresem tego równania będzie okrąg. Trzeba jednak przekształcić powyższe równanie do postaci kanonicznej.

Grupujemy wyrazy: $x^{2} - 6 x + y^{2} - 2 y + 6 = 0$ .

Aby skorzystać ze wzorów skróconego mnożenia, musimy jeszcze mieć wyrazy wolne, możemy więc dodać je do obu stron równania.

$(x^{2} - 6 x + 9) + (y^{2} - 2 y + 1) + 6 = 9 + 1$

$(x - 3)^{2} + (y - 1)^{2} = 10 - 6$

$(x - 3)^{2} + (y - 1)^{2} = 2^{2}$

Teraz wyraźnie widać, że rozwiązaniem równania jest zbiór par liczb, będących współrzędnymi punktów należących do okręgu o promieniu $r = 2$ i środku $S (3, 1)$ .

wykres

Pytania

Jak sprawdzić, czy podane równanie jest równaniem okręgu?

Jeżeli równanie da się przekształcić do postaci kanonicznej okręgu, to znaczy, że dane równanie jest nim. Gdy tylko obie niewiadome nie są w drugiej potędze lub występuje ich iloczyn, można podejrzewać, że dane równanie nie jest równaniem okręgu.

Zadania z rozwiązaniami

Zadanie nr 1.

Rozwiązać graficznie równanie $x^{2} + y^{2} + 4 x + 6 y + 9 = 0$ .

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Napisać równanie okręgu, który został zilustrowany na poniższym rysunku.

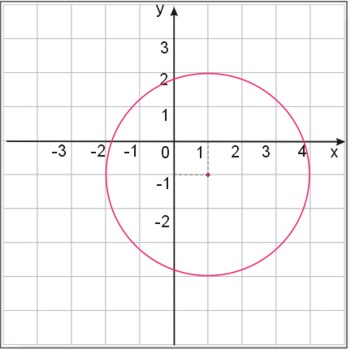
okrąg w układzie współrzędnych

Pokaż rozwiązanie zadania.

Zadanie nr 3.

Rozwiązać graficznie równanie $x y - 1 = 0$ .

Pokaż rozwiązanie zadania.

Zadanie nr 4.

Rozwiązać graficznie równanie $2 x^{2} + y + x - 1 = 0$ .

Pokaż rozwiązanie zadania.

Zadanie nr 5.

Znaleźć równanie okręgu opisanego na trójkącie równobocznym, wyznaczonym przez punkty $A = (1, 1), B = (5, 1), C = (3, 2 \sqrt{3} + 1)$ .

Pokaż rozwiązanie zadania.

Zadanie nr 6 — maturalne.

Wykaż, że dla dowolnych dodatnich liczb rzeczywistych $x$ i $y$ takich, że $x^{2} + y^{2} = 2$ , prawdziwa jest nierówność $x + y \leq 2$ .

Pokaż rozwiązanie zadania.

Zadanie nr 7 — maturalne.

Liczba punktów wspólnych okręgu o równaniu $(x + 2)^{2} + (y - 3)^{2} = 4$ z osiami układu współrzędnych jest równa:

A. 0

B. 1

C. 2

D. 4

Pokaż rozwiązanie zadania.

Zadanie nr 8 — maturalne.

Dany jest okrąg o środku $S = (2, 3)$ i promieniu $r = 5$ . Który z podanych punktów leży na tym okręgu?

A. $A = (- 1, 7)$

B. $B = (2, 3)$

C. $C = (3, 2)$

D. $D = (5, 3)$

Pokaż rozwiązanie zadania.

Zadanie nr 9 — maturalne.

Wyznacz równanie okręgu przechodzącego przez punkty $A = (- 5, 3)$ i $B = (0, 6)$ , którego środek leży na prostej o równaniu $x - 3 y + 1 = 0$ .

Pokaż rozwiązanie zadania.

Zadanie nr 10 — maturalne.

Średnicą okręgu jest odcinek $K L$ , gdzie $K = (6, 8)$ , $L = (- 6, - 8)$ . Równanie tego okręgu ma postać

A. $x^{2} + y^{2} = 200$

B. $x^{2} + y^{2} = 100$

C. $x^{2} + y^{2} = 400$

D. $x^{2} + y^{2} = 300$

Pokaż rozwiązanie zadania.

Zadanie nr 11 — maturalne.

Dane są okręgi o równaniach $x^{2} + y^{2} - 12 x - 8 y + 43 = 0$ i $x^{2} + y^{2} - 2 a x + 4 y + a^{2} - 77 = 0$ . Wyznacz wszystkie wartości parametru $a$ , dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.

Pokaż rozwiązanie zadania.

Zadanie nr 12.

Dany jest punkt $A = (- 1, 1)$ . Znaleźć punkt $B$ , jeżeli wiadomo, że $| \vec{A B} | = 4$ .

Pokaż rozwiązanie zadania.

Powiązane materiały

Nierówność drugiego stopnia z dwiema niewiadomymi

Równania i nierówności 2st. z 2 niewiadomymi

Okrąg i koło

Ćwiczenia

Równanie okręgu