Sześcian

Sześcian jest to prostopadłościan, którego wszystkie krawędzie są równe.

sześcian

Inna nazwa sześcianu to heksaedr.

Objętość sześcianu

Jak obliczyć objętość sześcianu?

Sześcian jest graniastosłupem, a objętość graniastosłupa obliczamy, mnożąc pole powierzchni podstawy (kwadratu) przez wysokość (długość krawędzi bocznej).

Wzór na objętość sześcianu jest następujący:

\(V=a^3\)

Przykład

Oblicz objętość sześcianu o krawędzi długości 2.

Stosujemy wprost wzór na objętość sześcianu i otrzymujemy: \(V=a^3=2^3=8\).

Pole powierzchni sześcianu

Jak obliczyć pole powierzchni sześcianu? Sześcian jest graniastosłupem, a pole powierzchni graniastosłupa obliczamy, dodając pola powierzchni podstawy i pola powierzchni ścian bocznych. Wzór na pole powierzchni sześcianu jest następujący:

\(P=6a^2\)

Aby zatem obliczyć pole sześcianu, wystarczy znać długość jego krawędzi.

Przykład

Oblicz pole sześcianu o krawędzi długości 2.

Stosujemy bezpośrednio wzór na pole powierzchni sześcianu i otrzymujemy: \(V=6a^2=6\cdot 2^2=24\).

Własności sześcianu

Sześcian jest przypadkiem wielościanu foremnego, gdyż wszystkie ściany są wielokątami foremnymi (kwadratami). Sześcian (heksaedr) ma sześć ścian kwadratowych, osiem wierzchołków i dwanaście krawędzi. Na sześcianie da się opisać kulę. Kulę też można wpisać w sześcian:

Promień kuli opisanej na sześcianie:

\(R=\frac{1}{2}a\sqrt{3}\)

Promień kuli wpisanej w sześcian:

\(r=\frac{1}{2}a\)

Przekątna sześcianu

Jak obliczyć przekątną sześcianu? Przekątna \(p\) tworzy z krawędzią długości \(a\), przekątną ściany o długości \(a\sqrt{2}\) przeciwprostokątną w trójkącie prostokątnym. Na podstawie twierdzenia Pitagorasa można obliczyć: \(p^2=a^2+(a\sqrt{2})^2\), a stąd \(p=a\sqrt{3}\).

Wzór na przekątną sześcianu:

\(p=a\sqrt{3}\)

Siatka sześcianu

Siatkę sześcianu przedstawia poniższa ilustracja. Siatka pozwala zrobić sześcian z papieru, poprzez zagięcie i sklejenie wspólnych wolnych krawędzi. Warto dodać, że nie jest to jedyna możliwa siatka sześcianu. Ile różnych siatek ma sześcian? Jest ich 11.

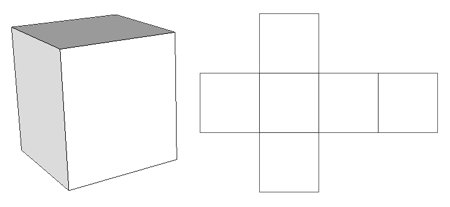
siatka sześcianu

Jak zrobić sześcian z papieru? Gotowy szablon siatki sześcianu do druku i sklejenia znajdziesz na końcu artykułu w formacie PDF w formie karty pracy.

Pytania

Ile krawędzi ma sześcian?

Sześcian ma 12 krawędzi.

Ile wierzchołków ma sześcian?

Sześcian ma 8 wierzchołków.

Ile ścian ma sześcian?

Jak sama nazwa mówi, sześcian ma sześć ścian.

Jakie pole powierzchni ma sześcian o przekątnej długości \(p\)?

Wyżej wyznaczona zależność między przekątną a długością krawędzi \(a\) może być wykorzystana do obliczenia objętości \(V=a^3=(\frac{p}{\sqrt{3}})^3 =\frac{\sqrt{3}p^3}{9}\).

Czy sześcian jest prostopadłościanem?

Tak, każdy sześcian jest prostopadłościanem, ale nie każdy prostopadłościan jest sześcianem.

Zadania z rozwiązaniami

Zadanie nr 1.

Ile osób może zagłosować, używając kulek o średnicy 1 cm, wrzucając je do urny o wymiarach 1 m x 1 m x 1 m?

Pokaż rozwiązanie zadania.

Zadanie nr 2.

Przekątna sześcianu ma długość równą \(\sqrt{3}\). Oblicz objętość tego sześcianu.

Pokaż rozwiązanie zadania.

Zadanie nr 3 — maturalne.

Przekątna sześcianu ma długość \(4\sqrt{3}\). Pole powierzchni tego sześcianu jest równe

A. 96

B. \(24\sqrt{3}\)

C. 192

D. \(16\sqrt{3}\)

Pokaż rozwiązanie zadania.

Zadanie nr 4 — maturalne.

Dany jest sześcian \(ABCDEFG\) o krawędzi długości \(a\). Punkty \(E, F, G, B\) są wierzchołkami ostrosłupa \(EFGB\) (zobacz rysunek).

Zadanie 26, matematyka, matura 2022

Pole powierzchni całkowitej ostrosłupa \(EFGB\) jest równe

A. \(a^2\)

B. \(\frac{3\sqrt{3}}{2}\cdot a^2\)

C. \(\frac{3}{2}\cdot a^2\)

D. \(\frac{3+\sqrt{3}}{2}\cdot a^2\)

Pokaż rozwiązanie zadania.

Zadanie nr 5 — maturalne.

Dany jest sześcian \(ABCDEFGH\) o krawędzi długości 6. Punkt \(S\) jest punktem przecięcia przekątnych \(AH\) i \(DE\) ściany bocznej \(ADHE\) (zobacz rysunek).

Zadanie 7, matura z matematyki rozszerzona 2023