Trapez
Co to jest trapez? Oto definicja trapezu:
Jak wygląda trapez? Na poniższym rysunku przedstawiono różne trapezy.

Podstawy trapezu
Podstawy trapezu to równoległe boki trapezu, natomiast pozostałe boki nazywamy ramionami.

Własności trapezu
Poniżej opisujemy kilka własności tej figury geometrycznej.
Środkowa trapezu
Środkowa trapezu jest to odcinek łączący środki ramion trapezu.

Twierdzenie
Środkowa trapezu jest równoległa do podstaw trapezu, a jej długość jest równa średniej arytmetycznej długości podstaw tego trapezu.
\(|MN|=\frac{|AB|+|CD|}{2}\)
Wysokość w trapezie
Wysokość trapezu jest to odcinek łączący dowolny wierzchołek trapezu z jego rzutem prostokątnym na podstawę lub jej przedłużenie, która nie zawiera tego wierzchołka. Wysokość najczęściej oznaczamy literą \(h\).

Rodzaje trapezów
Rozróżniamy kilka rodzajów trapezów w zależności od tego, jakie kryterium klasyfikacji przyjmiemy. Oto niektóre rodzaje trapezu.
Trapez równoramienny
Co to jest trapez równoramienny? Jeżeli ramiona trapezu są równe i nierównoległe, to taki trapez nazywamy trapezem równoramiennym.
Kąty w trapezie równoramiennym
Kąty wewnętrzne trapezu równoramiennego, jakie tworzą ramiona z dowolną podstawą, mają równe miary.
Twierdzenie
W trapezie równoramiennym przekątne mają równe długości.
Trapez prostokątny
Jeżeli jeden z kątów wewnętrznych trapezu jest kątem prostym, to taki trapez nazywamy prostokątnym. W takim trapezie jeszcze drugi kąt musi być kątem prostym.
Poniższy rysunek przedstawia wyżej wymienione rodzaje trapezów.

Pole i obwód trapezu
W następnym artykule pokazujemy jak obliczyć pole powierzchni trapezu oraz jego obwód.
Okrąg opisany na trapezie
Okrąg opisany na trapezie jest to okrąg, do którego należą wszystkie wierzchołki tego wielokąta. Mówimy też, że trapez jest wpisany w okrąg.
Okrąg można opisać na trapezie wtedy i tylko wtedy, gdy sumy miar przeciwległych kątów są równe.
Na każdym trapezie równoramiennym można opisać okrąg. Aby wyznaczyć środek okręgu opisanego na trapezie, należy wyznaczyć punkt przecięcia się symetralnych dwóch boków trapezu (przynajmniej jednego ramienia).
Okrąg wpisany w trapez
W trapez można wpisać okrąg, gdy sumy długości jego przeciwległych boków są równe.
Pytania
Ile ramion ma trapez?
Trapez ma dwa ramiona.
Czy prostokąt jest trapezem?
Trapez jest to czworokąt, który ma co najmniej jedną parę boków równoległych. Prostokąt spełnia ten warunek, zatem prostokąt jest trapezem. Jednak nie każdy trapez jest prostokątem.
Czy kwadrat jest trapezem?
Tak.
Czy każdy czworokąt jest trapezem?
Nie. Na przykład deltoid nie jest trapezem.
Jak inaczej nazywa się trapez prostokątny równoramienny?
To prostokąt.
Co to jest trapez równoboczny?
Trapez równoboczny jest kwadratem.
Co to jest trapez równoległoboczny?
Trapez równoległoboczny to taki trapez, którego ramiona i jedna z podstaw mają równe długości.
Co to jest trapezoid?
Trapezoid jest to czworokąt wypukły, który nie ma boków równoległych.
Czy istnieje wzór na wysokość trapezu?
Wysokość w trapezie wyliczamy zwykle z różnych jego własności w zależności od posiadanych danych, korzystając z twierdzenia Pitagorasa lub trygonometrii.
Ile wynosi suma kątów w trapezie?
Suma miar kątów wewnętrznych w trapezie wynosi 360°.
Ile ramion ma trapez?
Trapez ma dwa ramiona.
Zadania z rozwiązaniami

Zadanie nr 1.
Długość jednej z podstaw trapezu jest dwa razy większa od długości drugiej podstawy. Długość środkowej równoległej do podstaw jest równa 3. Obliczyć długości podstaw tego trapezu.

Zadanie nr 2.
W trapezie prostokątnym długość podstaw jest równa odpowiednio 3 i 6, a długość krótszego z ramion 2. Oblicz długość dłuższego ramienia trapezu.

Zadanie nr 3 — maturalne.
Punkt \(C=(0,2)\) jest wierzchołkiem trapezu \(ABCD\), którego podstawa AB jest zawarta w prostej o równaniu \(y=2x-4\). Wskaż równanie prostej zawierającej podstawę \(CD\).
A. \(y=\frac{1}{2}x+2\)
B. \(y=-2x+2\)
C. \(y=-\frac{1}{2}x+2\)
D. \(y=2x+2\)

Zadanie nr 4 — maturalne.
Wysokość trapezu równoramiennego o kącie ostrym 60° i ramieniu długości \(2\sqrt{3}\) jest równa:
A. \(\sqrt{3}\)
B. \(3\)
C. \(2\sqrt(3)\)
D. \(2\)

Zadanie nr 5 — maturalne.
Dany jest trapez prostokątny \(KLMN\), którego podstawy mają długości \(KL=a, MN=b,
a>b\). Kąt \(KLM\) ma miarę 60°. Długość ramienia \(LM\) tego trapezu jest równa:

A. \(a-b\)
B. \(2(a-b)\)
C. \(a+\frac{b}{2}\)
D. \((a+b)/2\)

Zadanie nr 6 — maturalne.
W trapezie prostokątnym \(ABCD\) dłuższa podstawa \(AB\) ma długość 8. Przekątna AC tego trapezu ma długość 4 i tworzy z krótszą podstawą trapezu kąt o mierze (zobacz rysunek). Oblicz długość przekątnej \(BD\) tego trapezu.


Zadanie nr 7 — maturalne.
Podstawą ostrosłupa czworokątnego ABCDS jest trapez \(ABCD (AB||CD)\). Ramiona tego trapezu mają długości \(AD=10\) i \(BC=16\), a miara kąta \(ABC\) jest równa 30°. Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt α, taki, że \(tg\alpha =\frac{9}{2}\). Oblicz objętość tego ostrosłupa.
Powiązane materiały
 Trapez
Trapez© medianauka.pl, 2010-11-23, A-1024
Data aktualizacji artykułu: 2023-06-24

 Pole i obwód trapezu
Pole i obwód trapezu Równoległobok
Równoległobok Pole równoległoboku
Pole równoległoboku Romb
Romb Pole rombu
Pole rombu Deltoid
Deltoid Inne czworokąty
Inne czworokąty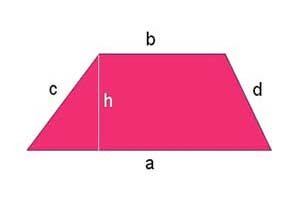 Pole trapezu — quiz
Pole trapezu — quiz