Wielokąty
Definicja
Wielokąt jest to figura geometryczna, która jest sumą łamanej zwyczajnej zamkniętej i części płaszczyzny ograniczonej tą łamaną.
Łamana stanowi brzeg wielokąta. Wierzchołki łamanej to wierzchołki wielokąta, natomiast boki łamanej, która wyznacza ten wielokąt, to boki wielokąta.
Rodzaje wielokątów
Oto przykłady wielokątów: trójkąty, kwadraty, prostokąty, wielokąty foremne, wielokąty nieforemne i inne. Omawiamy je w osobnych artykułach.
Właściwości wielokątów
Przekątna wielokąta to każdy odcinek niebędący bokiem wielokąta, łączący dwa wierzchołki tego wielokąta.
Poniższy rysunek przedstawia wszystkie przekątne (kolor niebieski) danego wielokąta.
Liczba przekątnych wielokąta
W dowolnym wielokącie wypukłym stosunek liczby przekątnych \(p\) do liczby boków \(n\) jest następujący:
Jest to wzór na liczbę przekątnych w wielokącie.
Przykłady
- Kwadrat ma \(n=4\) boki i \(p=\frac{4\cdot (4-3)}{2}=2\) przekątne.
- Sześciokąt wypukły ma \(n=6\) boków i \(p=\frac{6\cdot (6-3)}{2}=\frac{18}{2}=9\) przekątnych.
Przypomnijmy, że wielokąt wypukły to taka figura, w której każdy odcinek o końcach należących do tej figury zawiera się w tej figurze.
Definicja
Obwód wielokąta jest to suma długości boków wielokąta.
Kąty w wielokątach
Kąt wewnętrzny wielokąta wypukłego jest to kąt wypukły, w którego ramionach zawierają się dwa sąsiednie boku wielokąta.
Na powyższym rysunku zaznaczono wszystkie kąty wewnętrzne wielokąta \(ABCD\).
Twierdzenie
Wielokąt jest wypukły wtedy i tylko wtedy, gdy wszystkie jego kąty wewnętrzne są wypukłe.
Kąt zewnętrzny wielokąta wypukłego jest to każdy kąt przyległy do kąta wewnętrznego tego wielokąta.
Na rysunku zaznaczono kolorem niebieskim kąty zewnętrzne wielokąta.
Suma miar kątów w wielokącie
Ile wynosi suma kątów wewnętrznych?
Twierdzenie
- Suma kątów wewnętrznych w trójkącie jest kątem półpełnym.
- Suma miar kątów wewnętrznych w trójkącie jest równa 180°.
Możemy też napisać:
Przykład
W trójkącie prostokątnym jeden z kątów ma miarę równą 30°. Wyznacz pozostałe katy wewnętrzne tego trójkąta.
Ponieważ mamy do czynienia z trójkątem prostokątnym, więc jeden z jego kątów ma miarę 90°. Korzystając z powyższego twierdzenia mamy:
\(90°+30°+x=180°\)
\(x=180°-90°-30°\)
\(x=60°\)
Twierdzenie
Suma miar kątów wewnętrznych w czworokącie wypukłym jest równa 360°.
Twierdzenie
Suma miar kątów wewnętrznych w n-kącie wypukłym jest równa (n-2)·180°.
Szkic dowodu
Poniżej szkic dowodu powyższego twierdzenia.
Można wykazać, że każdy n-kąt wypukły można podzielić na (n-2) trójkątów (patrz na rysunek), których suma miar kątów wewnętrznych wynosi 180°. Zatem można w ten sposób wykazać prawdziwość ostatniego z zaprezentowanych tutaj twierdzeń.
Twierdzenie o okręgu opisanym w czworokąt
Warunkiem koniecznym i wystarczającym na to, aby w okrąg można było wpisać czworokąt, jest warunek, aby sumy przeciwległych kątów były równe.
Twierdzenie o okręgu wpisanym w czworokąt
Warunkiem koniecznym i wystarczającym na to, aby w czworokąt można było wpisać okrąg, jest warunek, aby sumy długości przeciwległych boków były równe.
Pytania
Jak obliczyć pole wielokąta nieforemnego?
Taki wielokąt można podzielić na trójkąty. Pole wielokąta będzie sumą pól powierzchni tych trójkątów.
Ile przekątnych ma wielokąt wypukły o 12 bokach?
Liczbę przekątnych w wielokącie wypukłym można obliczyć na podstawie wzoru p=n(n-3)/2. Zatem wielokąt wypukły o 12 bokach ma p=12·(12-3)/2=54 przekątne.
Co to jest wielokąt niewypukły?
Wielokąt, który nie jest wypukły, nazywamy niewypukłym.
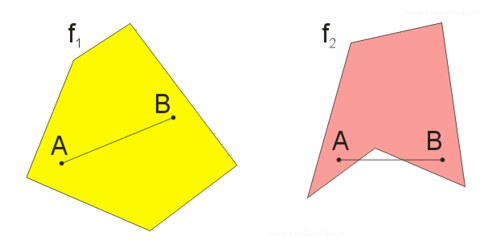
Na powyższym rysunku przedstawiono przykład wielokąta wypukłego (po lewej) oraz wielokąta niewypukłego (po prawej).
Jak skonstruować wielokąt foremny?
Na to pytanie odpowiadamy tutaj.
Co to jest wielokąt foremny?
Wielokąty foremne, a także wzory z nimi związane, omawiamy w odrębnym artykule (Link na końcu artykułu).
Czy trójkąt jest wielokątem?
Tak.
Zadania z rozwiązaniami
Zadanie nr 1.
Miara kąta wewnętrznego (pomiędzy sąsiednimi bokami) pewnego wielokąta foremnego jest równa 162°. Ile boków ma ten wielokąt?
Zadanie nr 2.
Obliczyć miarę kąta wewnętrznego (pomiędzy sąsiednimi bokami) n-kąta foremnego.
Zadanie nr 4 — maturalne.
Punkty \(A, B, C\) i \(D\) leżą na okręgu o środku S. Miary kątów \(SBC, BCD, CDA\) są równe odpowiednio: \(|\angle SBC|=60°, |\angle BCD|=110°, |\angle CDA|=90°\) (zobacz rysunek).
Wynika stąd, że miara \(\alpha\); kąta \(DAS\) jest równa
A. 25°
B. 30°
C. 35°
D. 40°
Zadanie nr 5 — maturalne.
Czworokąt \(ABCD\), w którym \(|BC|=4\) i \(|CD=5|\), jest opisany na okręgu. Przekątna \(AC\) tego czworokąta tworzy z bokiem \(BC\) kąt o mierze 60°, natomiast z bokiem \(AB\) – kąt ostry, którego sinus jest równy \(\frac{1}{4}\) . Oblicz obwód czworokąta \(ABCD\). Zapisz obliczenia.
Powiązane materiały
Wielokąt foremny
Trójkąty
Czworokąty
Figura geometryczna
Twierdzenie Talesa
Wielokąt© medianauka.pl, 2010-10-30, A-998
Data aktualizacji artykułu: 2023-06-08