Wykres funkcji homograficznej
Wykresem funkcji homograficznej jest hiperbola lub prosta (w szczególnym przypadku). W niniejszym artykule będzie nas interesowała jedynie hiperbola.
Zacznijmy od najprostszego przypadku. Wykreślimy wykres funkcji \(y=\frac{1}{x}\). Dziedziną tej funkcji jest \(\mathbb{R}\setminus\lbrace 0\rbrace \). Czyli dla zera funkcja nie jest określona. Sporządźmy tabelkę zmienności.
| \(x\) | -3 | -2 | -1 | -1/2 | -1/3 | 1/3 | 1/2 | 1 | 2 | 3 | 4 |
| \(y\) | \(-\frac{1}{3}\) | \(-\frac{1}{2}\) | -1 | -2 | -3 | 3 | 2 | 1 | \(\frac{1}{2}\) | \(\frac{1}{3}\) | \(\frac{1}{4}\) |
Na podstawie wypełnionej tabelki sporządzamy szkic wykresu funkcji (hiperboli).
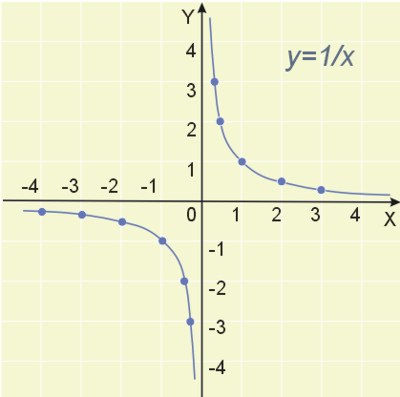
Widzimy, że funkcja jest malejąca w całej swojej dziedzinie.
Na poniższej ilustracji widzimy szkic wykresu funkcji \(y=-\frac{1}{x}\).

Widzimy, że funkcja jest rosnąca w całej swojej dziedzinie.
 Hiperbola — Wykres funkcji homograficznej online
Hiperbola — Wykres funkcji homograficznej online
Niniejsza symulacja ilustruje zachowanie hiperboli w zależności od wartości współczynnika a. Zmieniaj jego wartość za pomocą suwaka.
Funkcja w postaci y = a/x, czyli y =
a
1
Przesuwanie wykresu funkcji homograficznej
Aby sporządzić wykres funkcji homograficznej \(y=\frac{ax+b}{cx+d}\), korzystamy z przesunięcia wykresu funkcji o pewien wektor.
Doprowadzamy naszą funkcję do postaci \(y-v=\frac{m}{x-u}\) (poprzez podzielenie licznika przez mianownik — patrz dzielenie wielomianów) i przesuwamy wykres funkcji \(y=\frac{1}{x}\) o wektor \(\vec{w}=[u,v]\).
Przykłady
Sporządzić wykres funkcji \(y=\frac{2x+3}{x+3}\).
Dzielimy wielomiany:

Otrzymaliśmy resztę z dzielenia, więc możemy powyższą funkcję zapisać w postaci: \(y=2+\frac{-3}{x+3}\), czyli \(y-2=\frac{-3}{x+3}\).
Zatem, aby sporządzić wykres tej funkcji, musimy przesunąć wykres funkcji \(y=\frac{-3}{x}\) o wektor \(\vec{w}=[-3,2]\).
Na poniższej ilustracji kolorem czerwonym zaznaczono wykres właściwej funkcji. Linią przerywaną zaznaczono wykres funkcji \(y=\frac{-3}{x}\).

Zadania z rozwiązaniami

Zadanie nr 5 — maturalne.
Na rysunku przedstawiono fragment wykresu funkcji homograficznej f(x), której dziedziną jest zbiór \(D=(-\infty,3)\cup (3,+\infty)\).

Równanie \(|f(x)|=p\) z niewiadomą \(x\) ma dokładnie jedno rozwiązanie
A. w dwóch przypadkach: \(p=0\) lub \(p=3\).
B. w dwóch przypadkach: \(p=0\) lub \(p=2\).
C. tylko wtedy, gdy \(p=3\).
D. tylko wtedy, gdy \(p=2\).
Powiązane materiały
© medianauka.pl, 2009-08-20, A-292
Data aktualizacji artykułu: 2023-04-30


 Funkcja homograficzna
Funkcja homograficzna Funkcja wymierna i homograficzna
Funkcja wymierna i homograficzna