Wzory matematyczne
Oto wykaz najważniejszych wzorów matematycznych z podziałem na działy.
Obok znajdziesz arkusz z wzorami matematycznymi Centralnej Komisji Egzaminacyjnej CKE przydatne do matury.
Matematyka wzory
Wybrane wzory z matematyki:
Spis treści:
- Logika
- Teoria zbiorów
- Algebra
- Trygonometria
- Kombinatoryka, elementy statystyki i rachunek prawdopodobieństwa
- Analiza matematyczna
- Geometria
- Funkcje
Logika
Prawo tożsamości:
p ⇒ p
Prawo łączności koniunkcji i alternatywy:
((p ∧ q) ∧ r) ⇔ (p ∧ (q ∧ r))
((p ∨ q) ∨ r) ⇔ (p ∨ (q ∨ r))
Prawo rozdzielności koniunkcji względem alternatywy:
((p ∧ (q ∨ r)) ⇔ ((p ∨ q) ∧ (p ∨ r) ))
Prawa pochłaniania:
((p ∨ (q ∧ p)) ⇔ p
((p ∧ (q ∨ p)) ⇔ p
Prawa de Morgana:
\(\sim (p\land q)\Leftrightarrow (\sim p)\lor (\sim q)\)
\(\sim (p\lor q)\Leftrightarrow (\sim p)\land (\sim q)\)
Prawo wyłączonego środka:
\(p \vee \sim p\)
Prawo podwójnego zaprzeczenia/p>
\(\sim( \sim p ) \Leftrightarrow p\)
Prawo sprzeczności:
\(\sim (p \wedge \sim p)\)
Prawo Claviusa:
\((\sim p \Rightarrow p) \Rightarrow p\)
Prawo Dunsa Szkota:
\(\sim p \Rightarrow (p \Rightarrow q)\)
Zaprzeczenie implikacji
(~ (p ⇒ q) ) ⇔ ( p ∧ (~ q))
Prawo przechodniości implikacji:
[(p ⇒ q) ∧ (q ⇒ r)] ⇒ (p ⇒ r)
Zaprzeczenie równoważności:
~ (p ⇔ q) ⇔ ~ [(p ⇒ q) ∧ (q ⇒ p)]
Prawo przemienności równoważności:
(p ⇔ q) ⇔ (q ⇔ p)
Prawo przechodniości równoważności:
[(p ⇔ q) ∧ (q ⇔ r)] ⇒ (p ⇔ r)
Prawo kontrapozycji:
(p ⇒ q) ⇔ (~p ⇒ ~q)
Prawo odrywania:
[p ∧ (p ⇒ q)] ⇒ q
Teoria zbiorów
Prawa łączności:
\((A\cap B) \cap C = A\cap (B \cap C)\)
\((A\cup B) \cup C = A\cup (B \cup C)\)
Prawa przemienności:
\(A\cap B = B\cap A\)
\(A\cup B = B\cup A\)
Prawa rozdzielności:
\((A\cup B) \cap C = (A \cap C)\cup (B\cap C)\)
\((A\cap B) \cup C = (A \cup C)\cap (B\cup C)\)
Prawa absorpcji:
\(A\cap (A\cup B) = A\)
\(A\cup (A\cap B) = A\)
Prawa de Morgana dla zbiorów:
\((A\cup B)'=A'\cap B'\)
\((A\cap B)'=A'\cup B'\)
Inne:
\(A\cap A=A\)
\(A\cup A=A\)
\(A\cap A'=\emptyset \)
\(A\cup \emptyset = A \)
\(A×B \neq B×A\)
Algebra
Wartość bezwzględna
\(|x| = \begin{cases} x \ dla \ x \geq 0 \\ -x \ dla \ x<0 \end{cases}\)
Dla dowolnych liczb x i y:
\(|x+y|\leq |x|+|y|\)
\(|x-y|\leq |x|+|y| \)
\(|x\cdot y|=|x|\cdot |y| \)
Potęgi
\( a^{-n}=\frac{1}{a^n} \ dla \ a \in R \setminus \lbrace 0 \rbrace \wedge n \in N \)
Dla a≠0:
\(a^0=1\)
Dla nieujemnej liczby a oraz liczby naturalnej n określamy:
\(a^{\frac{1}{n}}=\sqrt[n]{a}\)
Dla nieujemnej liczby a oraz liczb naturalnych m i n określamy:
\(a^{\frac{m}{n}}=(a^{\frac{1}{n}})^m=\sqrt[n]{a^m}\)
Dla dodatniej liczby a oraz liczb naturalnych m i n określamy:
\(a^{-\frac{m}{n}}=(a^{\frac{1}{n}})^{-m}=\frac{1}{\sqrt[n]{a^m}}\)
Dla dodatnich wartości a i b oraz dowolnych liczb m i n:
\(a^m\cdot a^n = a^{m+n}\)
\(a^m:an = a^{m-n}, \ dla \ a \neq 0 \wedge m>n\)
\((a^m)^n = a^{m\cdot n}\)
\(a^n\cdot b^n = (ab)^n\)
\(a^n:b^n = (a:b)^n, \ dla \ b \neq 0\)
Pierwiastki
Pierwiastek stopnia n z liczby a, b ≥ 0 definiujemy:
\(\sqrt[n]{a}=b \Leftrightarrow b^n\)
\( \sqrt{a^2} = |a|\)
Jeżeli a ≥ 0, b ≥ 0, n ∈ N \ {0, 1}, to:
\( (\sqrt[n]{a})^n=a\)
\( \sqrt[n]{ab}=\sqrt[n]{a}\cdot \sqrt[n]{b}\)
\( \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}},\ b\neq 0\)
\( \sqrt[m]{\sqrt[n]{a}}=\sqrt[m\cdot n]{a}\)
\( (\sqrt[n]{a})^m=\sqrt[n]{a^m}\)
Wzory skróconego mnożenia
\((a+b)^2=a^2+2ab+b^2\)
\((a-b)^2=a^2-2ab+b^2\)
\(a^2-b^2=(a+b)(a-b)\)
\((a+b)^3=a^3+3a^2b+3ab^2+b^3\)
\((a-b)^3=a^3-3a^2b+3ab^2-b^3\)
\(a^3-b^3=(a-b)(a^2+ab+b^2)\)
\(a^3+b^3=(a+b)(a^2-ab+b^2)\)
Wzór dwumianowy Newtona:
\((a+b)^n={n \choose 0}a^n+{n \choose 1}a^{n-1}b+{n \choose 2}a^{n-2}b^2+...+{n \choose n}b^n\)
Logarytmy
Logarytmem liczby x>0 przy podstawie a, gdzie a>0 i a≠1 nazywamy wykładnik potęgi, do której należy podnieść liczbę a, aby otrzymać liczbę x.
\(\log_{a}x=y\Leftrightarrow a^y=x\)
Dla \(a\in R_+\) \{1} oraz \( b,c \in R_+\) prawdziwe są wszystkie poniższe zależności:
\(\log_{a}1=0\)
\(\log_{a}a=1\)
\(\log_{a}(b\cdot c)=\log_{a}b+\log_{a}c\)
\(\log_{a}\frac{b}{c}=\log_{a}b-\log_{a}c\)
\(\log_{a}b^n=n\cdot \log_{a}b\)
\(\log_{a}b=\frac{\log_{c}b}{\log_{c}a}\)
\(a^{\log_{a}b}=b\)
\(\log_{a}b=\frac{1}{\log_{b}a}\)
Silnia
\(0!=1\)
\(1!=1\)
\(n!=1\cdot{2}\cdot{3}...\cdot{n}\quad{dla}\quad{n}\geq{2}\)
\((n_1)!=n!(n+1)\)
Symbol Newtona
Niech \(n \in R, \ k \in N\) . Symbol Newtona, który oznaczamy \({n\choose k}\), a czytamy "n po k" jest to liczba wyrażona wzorem:
\({n\choose k}=\frac{n(n-1)(n-2)\cdot ...\cdot(n-k+1)}{k!}\)
gdy k jest większe od 0 oraz liczbę 1, gdy k=0.
Trygonometria
Tożsamości trygonometryczne
\(\sin^2{\alpha}+\cos^2{\alpha}=1\)
\(tg{\alpha}=\frac{\sin{\alpha}}{\cos{\alpha}}\)
\(ctg{\alpha}=\frac{\cos{\alpha}}{\sin{\alpha}}\)
\(tg{\alpha}=\frac{1}{ctg{\alpha}}\)
Funkcje sumy i różnicy kątów
\(\sin({\alpha+\beta})=\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}\)
\(\cos({\alpha+\beta})=\cos{\alpha}\cos{\beta}-\sin{\alpha}\sin{\beta}\)
\(tg({\alpha+\beta})=\frac{tg{\alpha}+tg{\beta}}{1-tg{\alpha}tg{\beta}}\)
\(ctg({\alpha+\beta})=\frac{ctg{\alpha}ctg{\beta}-1}{ctg{\alpha}+ctg{\beta}}\)
\(\sin({\alpha-\beta})=\sin{\alpha}\cos{\beta}-\cos{\alpha}\sin{\beta}\)
\(\cos({\alpha-\beta})=\cos{\alpha}\cos{\beta}+\sin{\alpha}\sin{\beta}\)
\(tg({\alpha-\beta})=\frac{tg{\alpha}-tg{\beta}}{1+tg{\alpha}tg{\beta}}\)
\(ctg({\alpha-\beta})=\frac{ctg{\alpha}ctg{\beta}+1}{ctg{\alpha}-ctg{\beta}}\)
Funkcje podwójnego i potrójnego kąta
\(\sin{2\alpha}=2\sin{\alpha}\cdot \cos{\alpha}\)
\(\cos{2\alpha}=\cos^2{\alpha}-\sin^2{\alpha}\)
\(tg{2\alpha}=\frac{2tg{\alpha}}{1-tg^2{\alpha}}\)
\(\sin{3\alpha}=3\sin{\alpha}-4\sin^3{\alpha}\)
\(\cos{3\alpha}=4\cos^3{\alpha}-3\cos{\alpha}\)
Funkcje połówkowego kąta
\(\sin{\frac{\alpha}{2}}=\pm\sqrt{\frac{1-\cos{\alpha}}{2}}\)
\(\cos{\frac{\alpha}{2}}=\pm\sqrt{\frac{1+\cos{\alpha}}{2}}\)
\(tg{\frac{\alpha}{2}}=\pm\sqrt{\frac{1-\cos{\alpha}}{1+\cos{\alpha}}}\)
\(tg{\frac{\alpha}{2}}=\frac{1-\cos{\alpha}}{\sin{\alpha}}=\frac{\sin{\alpha}}{1+\cos{\alpha}}\)
Sumy i różnice funkcji trygonometrycznych
\(\sin{\alpha}+\sin{\beta}=2\sin\frac{\alpha+\beta}{2}\cos{\frac{\alpha-\beta}{2}}\)
\(\sin{\alpha}-\sin{\beta}=2\cos\frac{\alpha+\beta}{2}\sin{\frac{\alpha-\beta}{2}}\)
\(\cos{\alpha}+\cos{\beta}=2\cos\frac{\alpha+\beta}{2}\cos{\frac{\alpha-\beta}{2}}\)
\(\cos{\alpha}-\cos{\beta}=-2\sin\frac{\alpha+\beta}{2}\sin{\frac{\alpha-\beta}{2}}\)
Wzory redukcyjne
| Dla kąta \(-\alpha\) |
| \(\sin{(-\alpha)}=-\sin{\alpha}\) |
| \(\cos{(-\alpha)}=\cos{\alpha}\) |
| \(tg{(-\alpha)}=-tg{\alpha}\) |
| \(ctg{(-\alpha)}=-ctg{\alpha}\) |
| Dla kąta 180°-α | Dla kąta 180°+α |
| \(\sin{(180^o-\alpha)}=\sin{\alpha}\) | \(\sin{(180^o+\alpha)}=-\sin{\alpha}\) |
| \(\cos{(180^o-\alpha)}=-\cos{\alpha}\) | \(\cos{(180^o+\alpha)}=-\cos{\alpha}\) |
| \(tg{(180^o-\alpha)}=-tg{\alpha}\) | \(tg{(180^o+\alpha)}=tg{\alpha}\) |
| \(ctg{(180^o-\alpha)}=-ctg{\alpha}\) | \(ctg{(180^o+\alpha)}=ctg{\alpha}\) |
| Dla kąta 90°-α | Dla kąta 90°+α |
| \(\sin{(90^o-\alpha)}=\cos{\alpha}\) | \(\sin{(90^o+\alpha)}=\cos{\alpha}\) |
| \(\cos{(90^o-\alpha)}=\sin{\alpha}\) | \(\cos{(90^o+\alpha)}=-\sin{\alpha}\) |
| \(tg{(90^o-\alpha)}=ctg{\alpha}\) | \(tg{(90^o+\alpha)}=-ctg{\alpha}\) |
| \(ctg{(90^o-\alpha)}=tg{\alpha}\) | \(ctg{(90^o+\alpha)}=-tg{\alpha}\) |
| Dla dowolnej liczby całkowitej k |
| \(\sin{(\alpha+k\cdot 360^o)}=\sin{\alpha}\) |
| \(\cos{(\alpha+k\cdot 360^o)}=\cos{\alpha}\) |
| \(tg{(\alpha+k\cdot 180^o)}=tg{\alpha}\) |
| \(ctg{(\alpha+k\cdot 180^o)}=ctg{\alpha}\) |
| Dla kąta 45°-α oraz 45°+α |
| \(\sin{(45^o+\alpha)}=\cos{(45^o-\alpha)}\) |
| \(\cos{(45^o+\alpha)}=\sin{(45^o-\alpha)}\) |
| \(tg{(45^o+\alpha)}=ctg{(45^o-\alpha)}\) |
| \(ctg{(45^o+\alpha)}=tg{(45^o-\alpha)}\) |
Elementy statystyki i rachunku prawdopodobieństwa
Kombinatoryka
\(0!=1\)
\(1!=1\)
\(n!=1\cdot{2}\cdot{3}...\cdot{n}\quad{dla}\quad{n}\geq{2}\)
\((n_1)!=n!(n+1)\)
Symbol Newtona
Niech \(n \in R, \ k \in N\) . Symbol Newtona, który oznaczamy \({n\choose k}\), a czytamy "n po k" jest to liczba wyrażona wzorem:
\({n\choose k}=\frac{n(n-1)(n-2)\cdot ...\cdot(n-k+1)}{k!}\)
gdy k jest większe od 0 oraz liczbę 1, gdy k=0.
Niech:
p - oznacza permutację, kombinację lub wariację,
n - liczba elementów pewnego zbioru,
k - liczba elementów ciągu lub podzbioru dla tworzonych p.
| nazwa p | Liczba p | Rodzaj | Czy kolejność wyrazów ma znaczenie? | Czy mogą występować powtórzenia tego samego elementu zbioru? |
| permutacje | \(P_n=n!\) | tworzymy ciągi n-elementowe | tak | nie |
| kombinacje | \(C^{k}_{n}={n \choose k}=\frac{n!}{k!(n-k)!}\) | tworzymy podzbiory k-elementowe | nie | nie |
| wariacje bez powtórzeń | \(V^{k}_{n}=\frac{n!}{(n-k)!}\) | tworzymy ciągi k-elementowe o różnych wyrazach | tak | nie |
| wariacje z powtórzeniami | \(W^{k}_{n}=n^k\) | tworzymy ciągi k-elementowe | tak | tak |
Rachunek prawdopodobieństwa
\(P(A)=\frac{\overline{\overline{A}}}{\overline{\overline{\Omega}}}\)
Prawdopodobieństwa warunkowe: \(P(A/ B)=\frac{P(A\cap B)}{P(B)}\)
Schemat Bernouliego:
\(P(S_n=k)={n\choose k}p^kq^{n-k}\)
\(p+q=1\)
- p - prawdopodobieństwo sukcesu w jednej próbie,
- q - prawdopodobieństwo porażki w jednej próbie.
Statystyka
Średnia arytmetyczna: \(\overline{x}=\frac{x_1+x_2+...+x_n}{n}\)
Średnia ważona: \(\overline{x}=\frac{x_1w_1+x_2w_2+...+x_nw_n}{w_1+w_2+...+w_n}\)
Mediana:
\(M=\begin{cases}x_{\frac{n+1}{2}}\ - \ dla\ n \ nieparzystego \\ \frac{1}{2}(x_{\frac{n}{2}}+x_{\frac{n}{2}+1})\ - \ dla \ n \ parzystego \end{cases}\)
Analiza matematyczna
Ciągi
Ciąg arytmetyczny
Ciąg (an) jest ciągiem arytmetycznym, jeżeli spełniony jest warunek:
\(a_{n+1}-a_n=r\)
Wzór na n-ty wyraz ciągu: \(a_n=a_1+(n-1)r\)
\(a_n=\frac{a_{n-1}+a_{n+1}}{2}\)
Wzór na sumę n początkowych wyrazów ciągu arytmetycznego.
\(S_n=\frac{a_{1}+a_{n}}{2}\cdot{n}\)
Ciąg geometryczny
Ciąg (an) jest ciągiem geometrycznym, jeżeli istnieje liczba \(q\neq 0\) i spełniony jest warunek:
\(\frac{a_{n+1}}{a_n}=q\)
Wzór na n-ty wyraz ciągu geometrycznego: \(a_n=a_1\cdot q^{n-1}\)
\(a_n=\sqrt{a_{n-1}\cdot a_{n+1}}\)
Suma wyrazów ciągu geometrycznego:
\(S_n=a_1\cdot{\frac{1-q^n}{1-q}} \ dla \ q\neq 1\)
\(S_n=a_1\cdot n, \ dla \ q=1\)
Granice ciągów
Niech \(\lim_{n\to\infty} a_n=a\) oraz \(\lim_{n\to\infty} b_n=b\). Prawdziwe są następujące równości:
\(\lim_{n\to\infty} (a_n+b_n)=a+b\)
\(\lim_{n\to\infty} (a_n-b_n)=a-b\)
\(\lim_{n\to\infty} (a_n\cdot b_n)=a\cdot b\)
\(\lim_{n\to\infty} \frac{a_n}{b_n}=\frac{a}{b},b_n\neq 0,b\neq 0\)
| Ciąg | Granica |
|---|---|
| \(a_n=\frac{1}{n}\) | \(\lim_{n\to\infty} \frac{1}{n}=0\) |
| \(a_n=\frac{k}{n}, \quad k\in R\) | \(\lim_{n\to\infty} \frac{k}{n}=0\) |
| Ciąg geometryczny: \(a_n=a_1\cdot q^{n-1}, \quad q< 0\) | \(\lim_{n\to\infty} a_1\cdot q^{n-1}=0\) |
| \(a_n=n^k, \quad k\in N_+\) | \(\lim_{n\to\infty} n^k=\infty\) |
| \(a_n=k^n, \quad k\in N_+\) | \(\lim_{n\to\infty} k^n=\infty\) |
| Ciąg stały: \(a_n=k, \quad k\in R\) | \(\lim_{n\to\infty} k=k\) |
Suma szeregu geometrycznego:
\(S=\frac{a_1}{1-q}\)
Granice funkcji
\(\lim_{x\to a}{c}=c\)
\(\lim_{x\to a}{x}=a\)
\(\lim_{x\to a}{\sqrt[n]{x}}=\sqrt[n]{a}, \ a> 0, \ n\in N\)
\(\lim_{x\to a}{\sin{x}}=\sin{a}\)
\(\lim_{x\to 0}{\frac{\sin{x}}{x}}=1\)
\(\lim_{x\to x_0}{[f(x)+g(x)]=a+b}\)
\(\lim_{x\to x_0}{[f(x)-g(x)]=a-b}\)
\(\lim_{x\to x_0}{[f(x)\cdot g(x)]=a\cdot b}\)
\(\lim_{x\to x_0}{[f(x):g(x)]=a:b (b\neq 0)}\)
\(\lim_{x\to x_0}{c\cdot f(x)}=c\cdot \lim_{x\to x_0}{f(x)}\)
Pochodne
\(f'(x_0)=\lim_{h\to 0}{\frac{f(x_0+h)-f(x_0)}{h}}\)
| Funkcja | Pochodna | Uwagi |
|---|---|---|
| c | 0 | \(x\in R\) |
| \(x^n\) | \(nx^{n-1}\) | \(x\in R, \ gdy \ n\in N\) \( x\in R_+, \ gdy \ n\in W\) |
| \(\sqrt{x}\) | \(\frac{1}{2\sqrt{x}}\) | \(x\in R_+\) |
| \(\frac{1}{x}\) | \(-\frac{1}{x^2}\) | \(x\neq 0\) |
| \(\sin{x}\) | \(\cos{x}\) | \(x\in R\) |
| \(\cos{x}\) | \(-\sin{x}\) | \(x\in R\) |
| \(tg{x}\) | \(\frac{1}{\cos^2{x}}\) | \(\cos{x}\neq 0\) |
| \(ctg{x}\) | \(-\frac{1}{\sin^2{x}}\) | \(\sin{x}\neq 0\) |
| \(a^x\) | \(a^x\cdot \ln{a}\) | \(a\in R_+\) |
| \(e^x\) | \(e^x\) | |
| \(\ln{x}\) | \(\frac{1}{x}\) | \(x>0\) |
| \(\log_{a}{x}\) | \(\frac{1}{x\ln{a}}\) | \(x>0, \ a>0, \ a\neq 1\) |
| \(\arcsin{x}\) | \(\frac{1}{\sqrt{1-x^2}}\) | \(|x|<1\) |
| \(\arccos{x}\) | \(-\frac{1}{\sqrt{1-x^2}}\) | \(|x|<1\) |
| \(arctg{x}\) | \(\frac{1}{1+x^2}\) | |
| \(arcctg{x}\) | \(\frac{-1}{1+x^2}\) |
| Nazwa | WZÓR |
|---|---|
| pochodna sumy | \([f(x)+g(x)]'=f'(x)+g'(x)\) |
| pochodna różnicy | \([f(x)-g(x)]'=f'(x)-g'(x)\) |
| pochodna iloczynu | \([f(x)\cdot g(x)]'=f'(x)g(x)+f(x)g'(x)\) |
| pochodna ilorazu | \([\frac{f(x)}{g(x)}]'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\) |
| mnożenie przez stałą | \([c\cdot f(x)]'=c\cdot f'(x)\) |
Pochodna funkcji złożonej: \(h'(x)=g'(f(x))\cdot f'(x)\)
Równanie stycznej do krzywej: \(y-y_0=f'(x_0)(x-x_0)\)
Całki
\(\int f(x)dx=F(x)+C\)
\(\int{dx}=x+C\)
\(\int{kdx}=kx+C\)
\(\int{x^ndx}=\frac{x^{n+1}}{n+1}+C,\quad{}a\neq-1,\quad{}x>0\)
\(\int{\frac{1}{x}dx}=\ln{|x|}+C,\quad{}x\neq{0}\)
\(\int{a^xdx}=\frac{a^x}{\ln{a}}+C,\quad{}a>0,\quad{}a\neq{1}\)
\(\int{\sin{x}dx}=-\cos{x}+C\)
\(\int{\cos{x}dx=\sin{x}+C}\)
\(\int{\frac{1}{\cos^{2}{x}}dx}=tgx+C,\quad{}\cos{x}\neq{0}\)
\(\int{\frac{1}{\sin^{2}{x}}dx}=-ctgx+C,\quad{}\sin{x}\neq{0}\)
\(\int{\frac{1}{\sqrt{1-x^2}}dx}=arcsinx+C,\quad{}-1<x<1\)
\(\int{\frac{1}{x^2+1}dx}=arctg+C\)
\(\int{[f(x)+g(x)]dx}=\int{f(x)dx}+\int{g(x)dx}\)
\(\int{kf(x)dx}=k\int{f(x)dx}\)
Całkowanie przez części: \(\int{udv}=uv-\int{vdu}\)
Geometria
Wektory
Długośc wektora
\(|\vec{a}|=\sqrt{a_x^2+a_y^2}\)
|\vec{AB}|=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)
Iloczyn skalarny
\(\vec{a}\circ \vec{b}=ab \cdot \cos{(\vec{a},\vec{b})}\)
\(\vec{a}\circ \vec{b}=a_xb_x+a_yb_y\)
Iloczyn wektorowy
\( |\vec{a} \times \vec{b}| = |\vec{a}| |\vec{b}| \sin \angle(\vec{a},\vec{b})\)
Odcinek
Długość odcinka: \(d=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}\)
Środek odcinka: \(x_s=\frac{x_A+x_B}{2},\quad{}y_s=\frac{y_A+y_B}{2}\)
Trójkąty
Wysokośc w trójkącie równobocznym: \(d=\frac{a\sqrt{3}}{2}\)
Pole tójkąta: \(P=\frac{1}{2}ah\)
lub \(P=\frac{1}{2}ab\sin{\gamma}\), gdzie γ jest katem między bokami a i b.
lub (wzór Herona): \(P=\sqrt{p(p-a)(p-b)(p-c)}, \ p=\frac{a+b+c}{2}\)
lub
\(W=\begin{vmatrix} a_x&a_y\\b_x&b_y \end{vmatrix}=a_xb_y-a_yb_x\)
\(P=\frac{1}{2}|W|\)
lub
\(P=\frac{1}{2}\begin{vmatrix} x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1 \end{vmatrix}\)
gdzie: \(P_1(x_1,y_1), \ P_2(x_2,y_2), \ P_3(x_3,y_3)\) są wierzchołkami trójkata.
Pole trójkąta równobocznego: \(P=\frac{a^2\sqrt{3}}{4}\)
Obwód trójkąta: \(L=a+b+c\)
Twierdzenie Pitagorasa
\(a^2+b^2=c^2\)
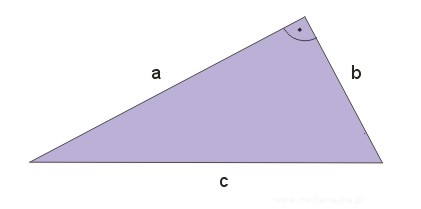
Twierdzenie sinusów i cosinusów
Twierdzenie sinusów:
\(\frac{a}{\sin{\alpha}}=\frac{b}{\sin{\beta}}=\frac{c}{\sin{\gamma}}=2R\)
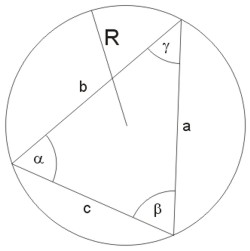
Twierdzenie cosinusów:
\(a^2=b^2+c^2-2bc\cos{\alpha}\)
\(b^2=a^2+c^2-2ac\cos{\beta}\)
\(c^2=a^2+b^2-2ab\cos{\gamma}\)
Twierdzenie tangensów:
\(\frac{a-b}{a+b}=\frac{tg\frac{\alpha-\beta}{2}}{tg\frac{\alpha+\beta}{2}}, \ \ \ \frac{b-c}{b+c}=\frac{tg\frac{\beta-\gamma}{2}}{tg\frac{\beta+\gamma}{2}}, \ \ \ \frac{a-c}{a+c}=\frac{tg\frac{\alpha-\gamma}{2}}{tg\frac{\alpha+\gamma}{2}}\)
Czworokąty
Prostokąt
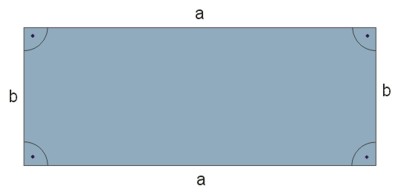
Przekątna prostokąta: \(d=\sqrt{a^2+b^2}\)
Pole prostokąta: \(P=ab\)
lub \(P=\frac{1}{2}d^2\sin{\gamma}\), gdzie kąt γ jest kątem między przekątnymi.
Obwód prostokąta: \(L=2a+2b\)
Kwadrat
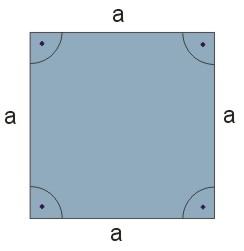
Przekątna kwadratu: \(d=a\sqrt{2}\)
Promień okręgu wpisanego w kwadrat \(r=\frac{a}{2}\)
Promień okręgu opisanego na kwadracie \(R=\frac{d}{2}=\frac{a\sqrt{2}}{2}\)
Pole kwadratu: \(P=a^2\)
lub \(P=\frac{1}{2}d^2\)
Obwód kwadratu: \(L=4a\)
Trapez
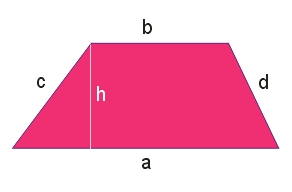
Pole trapezu: \(P=\frac{1}{2}(a+b)\cdot h\)
Obwód trapezu: \(L=a+b+c+d\)
Równoległobok
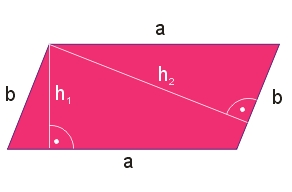
Pole równoległoboku: \(P=ah_1=bh_2\)
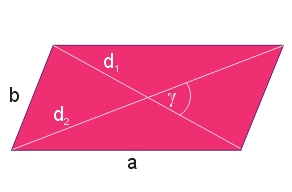
Pole równoległoboku: \(P=\frac{1}{2}d_1d_2\cdot \sin{\gamma}\)
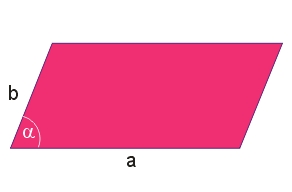
Pole równoległoboku: \(P=ab\cdot \sin{\alpha}\)
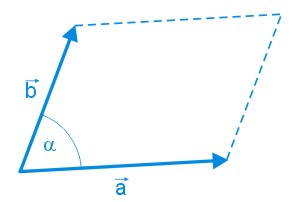
\(W=\begin{vmatrix} a_x&a_y\\b_x&b_y \end{vmatrix}=a_xb_y-a_yb_x\)
\(P=|W|\)
Obwód równoległoboku: \(L=2a+2b\)
Romb
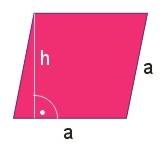
\(P=ah\)
\(L=4a\)
Deltoid
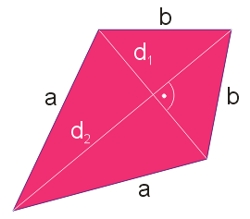
\(P=\frac{1}{2}d_1d_2\)
\(L=2a+2b\)
Okrąg, koło, elipsa
Równanie okręgu: (\(x-p)^2+(y-q)^2=r^2\)
Pole koła: \(P=\pi r^2\)
Długość okręgu: \(2\pi r\)
Równanie elipsy: \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
Mimośród elpisy: \(\varepsilon=\frac{c}{a}\)
Pole elipsy: \(P=\pi ab\)
Długość elipsy: \(L=4aE(\varepsilon)=2\pi a[1-(\frac{1}{2})^2\varepsilon ^2-(\frac{1\cdot 3}{2\cdot 4})^2 \cdot \frac{\varepsilon ^4}{3}-(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6})^2 \cdot \frac{\varepsilon ^6}{5}-...]\)
lub w przybliżeniu: \(L=\pi[\frac{3}{2}(a+b)-\sqrt{ab}]\)
Promień okręgu wpisanego w trójkąt: \(\frac{a}{2\sqrt{3}}\)
Promień okręgu opisanego na trójkącie: \(R=\frac{a}{\sqrt{3}}\)
Długość łuku okręgu: \(d=\frac{\alpha}{360}\cdot 2\pi r\)
Pole wycinka kołowego: \(P=\frac{\alpha}{360}\cdot \pi r^2\)
Wielokąty foremne
| Liczna n boków wielokąta |
Pole powierzchni wielokąta |
|---|---|
| 3 | \(\frac{a^2\sqrt{3}}{4}\) |
| 4 | \(a^2\) |
| 5 | \(\frac{a^2\sqrt{5}}{4}\sqrt{5+2\sqrt{5}}\) |
| 6 | \(\frac{3a^2\sqrt{3}}{2}\) |
| 8 | \(2a^2(1+\sqrt{2})\) |
| 10 | \(\frac{5a^2}{2}\sqrt{5+2\sqrt{5}}\) |
| Liczna n boków wielokąta |
Promień R okręgu opisanego na wielokącie |
Promień r okręgu wpisanego w wielokąt |
|---|---|---|
| 3 | \(\frac{a}{\sqrt{3}}\) | \(\frac{a}{2\sqrt{3}}\) |
| 4 | \(\frac{a^2\sqrt{3}}{4}\) | \(\frac{a}{2}\) |
| 5 | \(a^2\) | \(\frac{a}{2\sqrt{5}}\sqrt{5+2\sqrt{5}}\) |
| 6 | \(a\) | \(\frac{a\sqrt{3}}{2}\) |
| 8 | \(\frac{a}{\sqrt{2}}\sqrt{2+\sqrt{2}}\) | \(\frac{a}{2}(1+\sqrt{2})\) |
| 10 | \(2a^2(1+\sqrt{2})\) | \(\frac{a}{2}\sqrt{5+2\sqrt{5}}\) |
| Liczba boków | Miara kąta wewnętrznego |
|---|---|
| 3 | 60° |
| 4 | 90° |
| 5 | 108° |
| 6 | 120° |
| 7 | 128,(571428)° |
| 8 | 135° |
| 9 | 140° |
| 10 | 144° |
| 11 | 147,(27)° |
| 12 | 150° |
Bryły
| Bryła | Rysunek | Wzory na objętość pole powierzchni oraz promienie kuli wpisanej r i opisanej R na bryle. |
| sześcian | 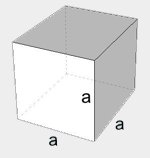 |
\(V=a^3\) \(P=6a^2\) \(R=\frac{1}{2}a\sqrt{3}\) \(r=\frac{1}{2}a\) |
| prostopadłościan | 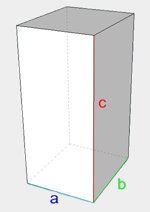 |
\(V=abc\) \(P=2ab+2ac+2bc\) |
| dowolny graniastosłup prosty i pochyły |
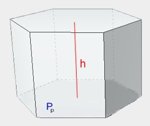 |
\(V=P_p\cdot h\) \(P=2P_p+P_b\) |
| czworościan foremny | 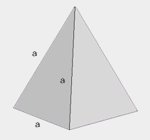 |
\(V=\frac{1}{12}a^3\sqrt{2}\) \(P=\sqrt{3}a^2\) \(R=\frac{1}{4}a\sqrt{6}\) \(r=\frac{1}{12}a\sqrt{6}\) |
| dowolny ostrosłup prosty lub pochyły |
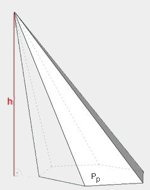 |
\(V=\frac{1}{3}P_p\cdot h\) \(P=P_p+P_b\) |
| piramida | 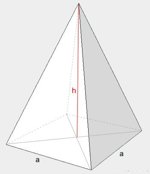 |
\(V=\frac{a^2h}{3}\) |
| ostrosłup ścięty | 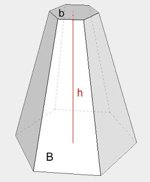 |
\(V=\frac{1}{3}h(B+\sqrt{Bb}+b)\) |
| ośmiościan foremny | 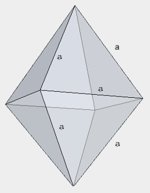 |
\(V=\frac{1}{3}a^3\sqrt{2}\) |
| dwunastościan foremny | 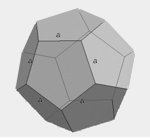 |
\(V=\frac{1}{4}a^3(15+7\sqrt{5})\) |
| dwudziestościan foremny |  |
\(V=\frac{5}{12}a^3(3+\sqrt{5})\) |
| walec | 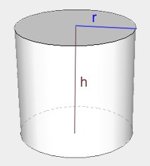 |
\(V=\pi r^2h\) \(P=2P_p+P_b=2\pi r^2+2\pi rh=2\pi r(r+h)\) |
| stożek | 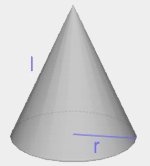 |
\(V=\frac{1}{3}\pi r^2h\) \(P=P_p+P_b=\pi r^2+\pi rl, \ l=\sqrt{r^2+h^2}\) |
| kula | 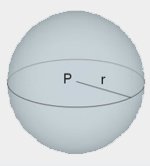 |
\(V=\frac{4}{3}\pi r^3\) \(S=4\pi R^2\) |
| Wielościan foremny | Promień kuli opisanej | Promień kuli wpisanej | Objętość wielościanu |
| czworościan | \(\frac{1}{4}a\sqrt{6}\) | \(\frac{1}{12}a\sqrt{6}\) | \(\frac{1}{12}a^3\sqrt{2}\) |
| sześcian | \(\frac{1}{2}a\sqrt{3}\) | \(\frac{1}{2}a\) | \(a^3\) |
| ośmiościan | \(\frac{1}{2}a\sqrt{2}\) | \(\frac{1}{6}a\sqrt{6}\) | \(\frac{1}{3}a^3\sqrt{2}\) |
| dwunastościan | \(\frac{1}{4}a\sqrt{18+6\sqrt{5}}\) | \(\frac{1}{4}a\sqrt{2}\sqrt{5+\frac{11}{5}\sqrt{5}}\) | \(\frac{1}{4}a^3(15+7\sqrt{5})\) |
| dwudziestościan | \(\frac{1}{4}a\sqrt{10+2\sqrt{5}}\) | \(\frac{1}{12}a\sqrt{3}\sqrt{3+\sqrt{5}}\) | \(\frac{5}{12}a^3(3+\sqrt{5})\) |
Funkcje
Funkcja kwadratowa
| Zagadnienie | Wzór |
| Postać ogólna funkcji kwadratowej | \(y=ax^2+bx+c\) |
| Postać iloczynowa funkcji kwadratowej | Postać iloczynowa: \(y=a(x-x_1)(x-x_2)\) Pierwiastki funkcji kwadratowej (miejsca zerowe funkcji kwadratowej): \(x_1=\frac{-b-\sqrt{\Delta}}{2a},\quad{x_2=\frac{-b+\sqrt{\Delta}}{2a}}\) Wyróżnik trójmianu kwadratowego: \(\Delta=b^2-4ac\) Miejsce zerowe funkcji kwadratowej, gdy \(\Delta=0\): \(x_0=-\frac{b}{2a}\) |
| Postać kanoniczna trójmianu kwadratowego | Postać kanoniczna: \(y=a(x+\frac{b}{2a})^2-\frac{\Delta}{4a}\) Wektor przesunięcia: \(\vec{u}=[-\frac{b}{2a},-\frac{\Delta}{4a}]\) Współrzędne wierzchołka paraboli: \(W(-\frac{b}{2a},-\frac{\Delta}{4a})\) |
| Wzory Viete'a | \(x_1+x_2=-\frac{b}{a}\) \(x_1\cdot{x_2}=\frac{c}{a}\) |
© medianauka.pl, 2022-01-02, A-4305

