Zadania — koła i okręgi
Znajdziesz tutaj zadania z działu koła i okręgi oraz elipsy. To zadania z rozwiązaniami. Są tu zadania autorskie oraz maturalne na poziomie podstawowym i rozszerzonym z kilku ostatnich lat.
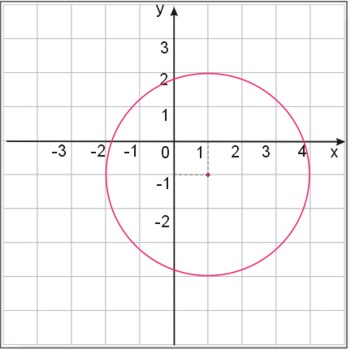
Zadanie nr 2.
Napisać równanie okręgu, który został zilustrowany na poniższym rysunku.
Zadanie nr 5.
Przez punkty \(A, B\) na okręgu o promieniu \(r=2,5\) poprowadzono średnicę. Punkt \(D\) leży na okręgu tak, że \(|BD|=4\). Oblicz odległość \(|AD|\).
Zadanie nr 6.
Na średnicy okręgu o promieniu długości 6 obrano punkt \(A\) w taki sposób, że punkt ten dzieli promień okręgu w stosunku 1 do 2 (krótszy odcinek znajduje się bliżej okręgu). Obliczyć obwód trójkątów wyznaczonych przez średnicę i odcinek prostopadłej przechodzący przez punkt \(A\).
Zadanie nr 10.
Ile potrzeba sznurka, aby ułożyć z niego okrąg o średnicy 2 m?
Zadanie nr 11.
Pole koła jest równe \(\pi\). Jaki promień ma koło o polu dwa razy mniejszym? Oblicz stosunek promieni tych okręgów.
Zadanie nr 12.
Z kwadratowej blachy o boku długości 1 m wycięto koła o promieniu \(r=10\ cm\) tak, że środki tych kół leżą na prostych równoległych i prostopadłych. Jaka jest powierzchnia ścinków? Jaki procent powierzchni blachy stanowią ścinki?
Zadanie nr 13.
W koło o promieniu \(r\) wpisano kwadrat. Oblicz pole figury, która stanowi różnicę tego koła i kwadratu?
Zadanie nr 14.
Na trójkącie równobocznym o boku \(a=1\) opisano okrąg. Oblicz obwód tego okręgu i pole koła wyznaczonego przez ten okrąg.
Zadanie nr 15.
W trójkąt równoboczny o boku długości \(a=1\) wpisano koło. Oblicz jego pole i obwód.
Zadanie nr 16.
Na trójkącie prostokątnym o przyprostokątnych długości 3 i 4 opisano koło. Oblicz pole i obwód tego koła.
Zadanie nr 17.
Znaleźć równanie okręgu opisanego na trójkącie równobocznym, wyznaczonym przez punkty \(A=(1,1), B=(5,1), C=(3,2\sqrt{3}+1)\).
Zadanie nr 18.
Jaka jest długość półosi wielkiej elipsy o równaniu \(x^2+16y^2=144\)? Sporządź szkic tej elipsy w układzie współrzędnych.
Zadanie nr 19.
Zaznaczyć w układzie współrzędnych ogniska elipsy o równaniu \(\frac{x^2}{4}+y^2=1\).
Zadanie nr 20.
Dana jest elipsa o równaniu \(x^2+4y^2=4\). Obliczyć mimośród tej elipsy.
Zadanie nr 21.
Dana jest elipsa o mimośrodzie \(\varepsilon=\frac{1}{2}\) i ognisku w punkcie \(F=(\frac{3}{2},0)\). Znaleźć równanie tej elipsy.
Zadanie nr 24.
Oblicz pole powierzchni elipsy, której półosie mają długości 6 i 5.
Zadanie nr 26.
Dany jest okrąg o równaniu \(x^2+y^2=4\). Długość półosi wielkiej pewnej elipsy jest równa długości promienia okręgu. Pole tej elipsy jest dwa razy mniejsze od pola koła wyznaczonego przez okrąg. Jaka jest długość drugiej półosi elipsy?
Zadanie nr 27.
Ile sznurka potrzeba do ułożenia elipsy o polu \(6\pi\) i osi wielkiej elipsy o długości 6.
Zadanie nr 28.
Znaleźć środek okręgu opisanego na trójkącie \(ABC\), gdzie \(A=(2,0), B=(1,2), C=(-2,-1)\).
Zadanie nr 30.
Oblicz długość okręgu danego równaniem \((x-1)^2+(y-1)^2=2\).
Zadanie nr 31.
Wyznaczyć środek okręgu wpisanego w trójkąt wyznaczony przez punkty \(A=(0,0), B=(4,0), C=(0,3)\).
Zadanie nr 32.
Obliczyć pole powierzchni pierścienia kołowego wyznaczonego przez okręgi \(x^2+y^2=4\) oraz \(x^2+y^2=16\).
Zadanie nr 33.
Pola dwóch kół współśrodkowych są równe odpowiednio 6 i 4. Oblicz pole pierścienia kołowego wyznaczonego przez te koła.
Zadanie nr 34.
Dany jest punkt \(A=(-1,1)\). Znaleźć punkt \(B\), jeżeli wiadomo, że \(|\vec{AB}|=4\).
Zadanie nr 35.
Obliczyć długość łuku wyznaczonego przez półokrąg o promieniu 4.
Zadanie nr 36.
Obliczyć długość łuku okręgu o kącie środkowym 30o i promieniu \(r=3\).
Zadanie nr 37.
Jaką miarę ma kąt środkowy, jeżeli długość łuku okręgu na nim opartego jest równa \(\frac{3}{4}\pi\), a promień tego okręgu ma długość 3?
Zadanie nr 38.
Jakie pole zakreśla na zegarze sekundnik w czasie 1 sekundy, jeżeli długość tej wskazówki jest równa 20 cm?
Zadanie nr 39.
Jaką część należy wyciąć z pierścienia kołowego, aby jego pole było równe \(\frac{\pi}{8}\)?

Zadanie nr 40 - maturalne.
Punkty \(ABCD\) leżą na okręgu o środku \(S\) (zobacz rysunek). Miara kąta \(BDC\) jest równa:

A. 91°
B. 72,5°
C. 18°
D. 32°

Zadanie nr 41 - maturalne.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych \(x\) i \(y\) takich, że \(x^2+y^2=2\), prawdziwa jest nierówność \(x+y\leq 2\).

Zadanie nr 42 - maturalne.
Miara kąta wpisanego w okrąg jest o \(20°\) mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa:
A. \(5°\)
B. \(10°\)
C. \(20°\)
D. \(30°\)

Zadanie nr 43 - maturalne.
Liczba punktów wspólnych okręgu o równaniu \((x+2)^2+(y-3)^2=4\) z osiami układu współrzędnych jest równa:
A. 0
B. 1
C. 2
D. 4

Zadanie nr 44 - maturalne.
Środek \(S\) okręgu opisanego na trójkącie równoramiennym \(ABC\), o ramionach \(AC\) i \(BC\), leży wewnątrz tego trójkąta (zobacz rysunek).

Wykaż, że miara kąta wypukłego \(ASB\) jest cztery razy większa od miary kąta wypukłego \(SBC\).

Zadanie nr 45 - maturalne.
Na okręgu o środku w punkcie \(O\) leży punkt \(C\) (zobacz rysunek). Odcinek \(AB\) jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy \(\alpha\) ma miarę:
A. \(m=116°
B. \(m=114°
C. \(m=112°
D. \(m=110°


Zadanie nr 46 - maturalne.
Dany jest okrąg o środku \(S=(2,3)\) i promieniu \(r=5\). Który z podanych punktów leży na tym okręgu?
A. \(A=(-1, 7)\)
B. \(B=(2, 3)\)
C. \(C=(3, 2)\)
D. \(D=(5, 3)\)

Zadanie nr 47 - maturalne.
W trójkącie równoramiennym wysokość opuszczona na podstawę jest równa 36, a promień okręgu wpisanego w ten trójkąt jest równy 10. Oblicz długości boków tego trójkąta i promień okręgu opisanego na tym trójkącie.

Zadanie nr 48 - maturalne.
Wyznacz równanie okręgu przechodzącego przez punkty \(A=(−5, 3)\) i \(B=(0, 6)\), którego środek leży na prostej o równaniu \(x−3y+1=0\).

Zadanie nr 49 - maturalne.
Dany jest okrąg o środku \(S\). Punkty \(K, L\) i \(M\) leżą na tym okręgu. Na łuku \(KL\) tego okręgu są oparte kąty \(KSL\) i \(KML\) (zobacz rysunek), których miary \(\alpha\) i \(\beta\), spełniają warunek \(\alpha +\beta=111°\). Wynika stąd, że

A. \(\alpha=74°\)
B. \(\alpha=76°\)
C. \(\alpha=70°\)
D. \(\alpha=72°\)

Zadanie nr 50 - maturalne.
Średnicą okręgu jest odcinek \(KL\), gdzie \(K=(6,8)\), \(L=(−6, − 8)\). Równanie tego okręgu ma postać
A. \(x^2+y^2=200\)
B. \(x^2+y^2=100\)
C. \(x^2+y^2=400\)
D. \(x^2+y^2=300\)

Zadanie nr 51 - maturalne.
Okręgi o środkach odpowiednio \(A\) i \(B\) są styczne zewnętrznie i każdy z nich jest styczny do obu ramion danego kąta prostego (zobacz rysunek). Promień okręgu o środku \(A\) jest równy 2.

Uzasadnij, że promień okręgu o środku \(B\) jest mniejszy od \(\sqrt{2}-1\).

Zadanie nr 52 - maturalne.
Trójkąt \(ABC\) jest ostrokątny oraz \(|AC|>|BC|\). Dwusieczna \(d_C\) kąta \(ACB\) przecina bok \(AB\) w punkcie \(K\). Punkt \(L\) jest obrazem punktu \(K\) w symetrii osiowej względem dwusiecznej \(d_A\) kąta \(BAC\), punkt \(M\) jest obrazem punktu \(L\) w symetrii osiowej względem dwusiecznej \(d_C\) kąta \(ACB\), a punkt \(N\) jest obrazem punktu \(M\) w symetrii osiowej względem dwusiecznej \(d_B\) kąta \(ABC\) (zobacz rysunek).

Udowodnij, że na czworokącie \(KNML\) można opisać okrąg.

Zadanie nr 53 - maturalne.
Punkty \(D\) i \(E\) leżą na okręgu opisanym na trójkącie równobocznym \(ABC\) (zobacz rysunek). Odcinek \(CD\) jest średnicą tego okręgu. Kąt wpisany \(DEB\) ma miarę \(\alpha\).

A. \(\alpha=30°\)
B. \(\alpha<30°\)
C. \(\alpha>45°\)
D. \(\alpha=45°\)

Zadanie nr 54 - maturalne.
Dane są okręgi o równaniach \(x^2+y^2−12x−8y+43=0\) i \(x^2+y^2−2ax+4y+a^2−77=0\). Wyznacz wszystkie wartości parametru \(a\), dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.

Zadanie nr 55 - maturalne.
Punkty \(A, B, C, D\) leżą na okręgu o środku w punkcie \(O\). Kąt środkowy \(DOC\) ma miarę 118° (zobacz rysunek).

Miara kąta ABC jest równa
A. 59°
B. 48°
C. 62°
D. 31°

Zadanie nr 56 - maturalne.
Pole figury \(F_1\) złożonej z dwóch stycznych zewnętrznie kół o promieniach 1 i 3 jest równe polu figury \(F_2\) złożonej z dwóch stycznych zewnętrznie kół o promieniach długości \(r\) (zobacz rysunek).

Długość \(r\) promienia jest równa
A. \(\sqrt{3}\)
B. \(2\)
C. \(\sqrt{5}\)
D. \(3\)

Zadanie nr 57 - maturalne.
Dany jest trójkąt prostokątny \(ABC\). Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta \(ABC\), który ma większą miarę.

Zadanie nr 58 - maturalne.
Punkty A, B, C leżą na okręgu o środku S. Punkt D jest punktem przecięcia cięciwy AC i średnicy okręgu poprowadzonej z punktu B. Miara kąta BSC jest równa α, a miara kąta ADB jest równa γ (zobacz rysunek).

Wtedy kąt ABD ma miarę
A. \(\frac{\alpha}{2}+\gamma−180°\)
B. \(180°-\frac{\alpha}{2}-\gamma\)
C. \(180°-\alpha-\gamma\)
D. \(\alpha+\gamma−180°\)

Zadanie nr 59 - maturalne.
Punkty \(A, B, P\) leżą na okręgu o środku \(S\) i promieniu 6. Czworokąt \(ASBP\) jest rombem, w którym kąt ostry \(PAS\) ma miarę 60° (zobacz rysunek).

Pole zakreskowanej na rysunku figury jest równe
A. \(6\pi\)
B. \(9\pi\)
C. \(10\pi\)
D. \(12\pi\)

Zadanie nr 60 - maturalne.
Punkty \(A, B, C\) leżą na okręgu o środku w punkcie \(O\). Kąt \(ACO\) ma miarę 70° (zobacz rysunek). Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Miara kąta ostrego \(ABC\) jest równa:

A. \(10°\)
B. \(20°\)
C. \(35°\)
D. \(40°\)
Liczba odnalezionych zadań w zbiorze: 60.
Oznaczenia
 Zadania maturalne — poziom podstawowy.
Zadania maturalne — poziom podstawowy.
 Zadania maturalne — poziom rozszerzony.
Zadania maturalne — poziom rozszerzony.






