Nauka » Matematyka » Trójkąt równoboczny Równanie okręgu

Zadanie - równanie okręgu

Znaleźć równanie okręgu opisanego na trójkącie równobocznym, wyznaczonym przez punkty $A=(1,1), \ B=(5,1),\ C=(3,2\sqrt{3}+1)$

Rozwiązanie zadania uproszczone

$A=(1,1), \ B=(5,1)\\ |AB|=a=4$
$h=\frac{\sqrt{3}}{2}a=2\sqrt{3}$
$r=\frac{2}{3}h=\frac{4\sqrt{3}}{3}$
$x_s=\frac{1+5}{2}=3$
$y_s=1+\frac{1}{3}h=1+\frac{2\sqrt{3}}{3}$
$(x-x_s)^2+(y-y_s)^2=r^2\\ (x-3)^2+(y-1-\frac{2\sqrt{3}}{3})^2=\frac{16}{3}$

Rozwiązanie zadania ze szczegółowymi wyjaśnieniami

Sporządzamy szkic:

Równanie okręgu o środku i promieniu r jest dane wzorem:

Musimy więc znaleźć współrzędne środka okręgu oraz jego promień. Ponieważ mamy do czynienia z okręgiem opisanym na trójkącie równobocznym, środek okręgu dzieli wysokość trójkąta na trzy równe części, więc:

$r=\frac{2}{3}h$

Wysokość trójkąta można wyznaczyć, znając długość boku. Długość boku można obliczyć na podstawie wzoru na odległość między dwoma punktami w układzie współrzędnych:

$|AB|=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$

Mamy więc dla punktów A i B:

$A=(1,1), \ B=(5,1)\\ |AB|=a=\sqrt{(5-1)^2+(1-1)^2}=4$

Obliczamy wysokość trójkąta, korzystając z twierdzenia Pitagorasa:

$h^2+(\frac{1}{2}a)^2=a^2\\ h^2=\frac{3}{4}a^2\\ h=\frac{\sqrt{3}}{2}a\\ a=4\\ h=\frac{\sqrt{3}}{2} \cdot 4=2\sqrt{3}$

a następnie promień:

$r=\frac{2}{3}h=\frac{2}{3}\cdot 2\sqrt{3}=\frac{4\sqrt{3}}{3}$

Aby wyznaczyć współrzędne środka okręgu posłużymy się wiedzą na temat środka okręgu opisanego na trójkącie, który leży na przecięciu się symetralnych boków trójkąta. Zatem współrzędna x środka okręgu jest taka sama jak współrzędna x środka odcinka AB. Środek odcinka wyznaczonego przez punkty w układzie współrzędnych obliczamy ze wzoru:

$x_s=\frac{x_A+x_B}{2}$

Mamy więc:

$x_s=x_O=\frac{1+5}{2}=3$

Środek okręgu leży o 1/3 wysokości nad podstawą trójkąta AB, która leży na prostej y=1. Współrzędna y środka okręgu spełnia więc zależność:

$y_s=1+\frac{1}{3}h=1+\frac{1}{3}\cdot 2\sqrt{3}=1+\frac{2\sqrt{3}}{3}$

Mamy już wszystkie dane, aby napisać równanie okręgu:

$(x-x_s)^2+(y-y_s)^2=r^2\\ (x-3)^2+(y-1-\frac{2\sqrt{3}}{3})^2=(\frac{4\sqrt{3}}{3})^2=\frac{16\cdot 3}{9}=\frac{16}{3}$

Odpowiedź

$(x-3)^2+(y-1-\frac{2\sqrt{3}}{3})^2=\frac{16}{3}$

Zadania podobne

Zadanie - równanie okręgu
Rozwiązać graficznie równanie

.

Pokaż rozwiązanie zadania

Zadanie - równanie okręgu - odczyt z wykresu
Napisać równanie okręgu, który został zilustrowany na poniższym rysunku.
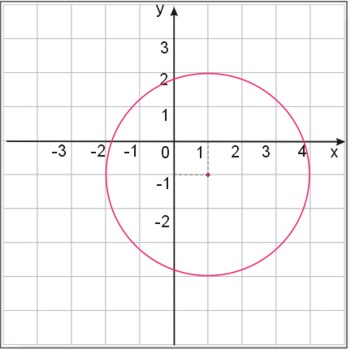
okrąg w układzie współrzędnych

Pokaż rozwiązanie zadania

Zadanie - równanie drugiego stopnia z dwiema niewiadomymi
Rozwiązać graficznie równanie

Pokaż rozwiązanie zadania

Zadanie - równanie drugiego stopnia z dwiema niewiadomymi
Rozwiązać graficznie równanie

Pokaż rozwiązanie zadania

Zadanie - długość wektora i równanie okręgu
Dany jest punkt A=(-1,1). Znaleźć punkt B jeżeli wiadomo, że $|\vec{AB}|=4$ .

Pokaż rozwiązanie zadania

Zadanie maturalne nr 8, matura 2016 (poziom rozszerzony)
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych x i y takich, że x²+y²=2, prawdziwa jest nierówność x +y ≤ 2.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 15, matura 2014
Liczba punktów wspólnych okręgu o równaniu (x+2)²+(y-3)²=4 z osiami układu współrzędnych jest równa:

A. 0
B. 1
C. 2
D. 4

Pokaż rozwiązanie zadania

Zadanie maturalne nr 20, matura 2017 (poziom podstawowy)
Dany jest okrąg o środku S = (2,3) i promieniu r = 5 . Który z podanych punktów leży na tym okręgu?
A. A = (-1, 7)
B. B = (2, 3)
C. C = (3, 2)
D. D = (5, 3)

Pokaż rozwiązanie zadania

Zadanie maturalne nr 11, matura 2017 (poziom rozszerzony)
Wyznacz równanie okręgu przechodzącego przez punkty A=(−5, 3) i B=(0, 6), którego środek leży na prostej o równaniu x−3y+1=0.

Pokaż rozwiązanie zadania

Zadanie maturalne nr 18, matura 2018

Średnicą okręgu jest odcinek KL, gdzie K = (6,8) , L = (−6, − 8) . Równanie tego okręgu ma
postać

x²+y²=200
x²+y²=100
x²+y²=400
x²+y²=300

Pokaż rozwiązanie zadania

Niektóre treści nie są dostosowane do Twojego profilu. Jeżeli jesteś pełnoletni możesz wyrazić zgodę na przetwarzanie swoich danych osobowych. W ten sposób będziesz miał także wpływ na rozwój naszego serwisu.