Zadanie - długość wektora i równanie okręgu
Treść zadania:
Dany jest punkt \(A=(-1,1)\). Znaleźć punkt \(B\), jeżeli wiadomo, że \(|\vec{AB}|=4\).
 Rozwiązanie zadania
Rozwiązanie zadania
Oznaczmy współrzędne punktu \(B\) przez \(B=(x,y)\). Wektor \(\vec{AB}\) ma wówczas współrzędne:
Powołujemy się na twierdzenie, że jeżeli wektor \(\vec{AB}=[a_x,a_y]\) leży na płaszczyźnie OXY, to zachodzą równości:
\(a_x=x_B-x_A\)
\(a_y=y_B-y_A\)
Powyższe twierdzenie pozwala nam wyznaczyć w prosty sposób współrzędne wektora, gdy dane są współrzędne jego początku \(A=(x_A,y_A)\) i końca \(B=(x_B,y_B)\). Możemy więc zapisać, że:
Korzystamy wprost z powyższego wzoru:
\(A=(-1,1), \ B=(x,y)\)
\(\vec{AB}=[x-(-1),y-1]=[x+1,y-1]\)
Korzystamy ze wzoru na długość wektora \(\vec{a}=[a_x,a_y]\)
Wiemy, że długość naszego wektora jest równa 4. Mamy więc:
\(|\vec{AB}|=\sqrt{(x+1)^2+(y-1)^2}=4 /^2\)
\((x+1)^2+(y-1)^2=4^2\)
Otrzymaliśmy równanie z dwoma niewiadomymi. Pamiętamy, że równanie w postaci:
jest równaniem okręgu o środku w punkcie \(S=(x_s,y_s)\) i promieniu \(r\). Zatem nasz punkt B to dowolny punkt okręgi o środku \(S=(-1,1)\) i promieniu \(r=4\).
 Odpowiedź
Odpowiedź
© medianauka.pl, 2011-03-05, ZAD-1199


Zadania podobne
Zadanie nr 2.
Napisać równanie okręgu, który został zilustrowany na poniższym rysunku.
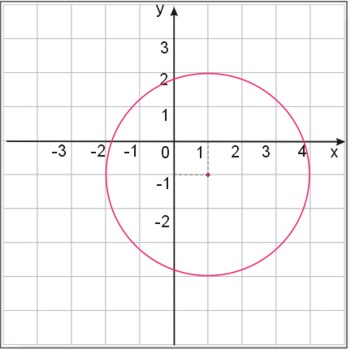
Zadanie nr 5.
Znaleźć równanie okręgu opisanego na trójkącie równobocznym, wyznaczonym przez punkty \(A=(1,1), B=(5,1), C=(3,2\sqrt{3}+1)\).

Zadanie nr 6 — maturalne.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych \(x\) i \(y\) takich, że \(x^2+y^2=2\), prawdziwa jest nierówność \(x+y\leq 2\).

Zadanie nr 7 — maturalne.
Liczba punktów wspólnych okręgu o równaniu \((x+2)^2+(y-3)^2=4\) z osiami układu współrzędnych jest równa:
A. 0
B. 1
C. 2
D. 4

Zadanie nr 8 — maturalne.
Dany jest okrąg o środku \(S=(2,3)\) i promieniu \(r=5\). Który z podanych punktów leży na tym okręgu?
A. \(A=(-1, 7)\)
B. \(B=(2, 3)\)
C. \(C=(3, 2)\)
D. \(D=(5, 3)\)

Zadanie nr 9 — maturalne.
Wyznacz równanie okręgu przechodzącego przez punkty \(A=(−5, 3)\) i \(B=(0, 6)\), którego środek leży na prostej o równaniu \(x−3y+1=0\).

Zadanie nr 10 — maturalne.
Średnicą okręgu jest odcinek \(KL\), gdzie \(K=(6,8)\), \(L=(−6, − 8)\). Równanie tego okręgu ma postać
A. \(x^2+y^2=200\)
B. \(x^2+y^2=100\)
C. \(x^2+y^2=400\)
D. \(x^2+y^2=300\)

Zadanie nr 11 — maturalne.
Dane są okręgi o równaniach \(x^2+y^2−12x−8y+43=0\) i \(x^2+y^2−2ax+4y+a^2−77=0\). Wyznacz wszystkie wartości parametru \(a\), dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.

