
Zadanie maturalne nr 18, matura 2018
Treść zadania:
Średnicą okręgu jest odcinek \(KL\), gdzie \(K=(6,8)\), \(L=(−6, − 8)\). Równanie tego okręgu ma postać
A. \(x^2+y^2=200\)
B. \(x^2+y^2=100\)
C. \(x^2+y^2=400\)
D. \(x^2+y^2=300\)
 Rozwiązanie zadania
Rozwiązanie zadania
KL jest średnicą okręgu. Ponieważ K i L są symetryczne względem początku układu współrzędnych, stąd wniosek, że środek okręgu leży właśnie w początku układu współrzędnych.
Promień tego okręgu będzie miało postać:
\( x^2+y^2=r^2 \)
Promień tego okręgu to długość odcinka OK, gdzie O=(0,0).
Skorzystamy ze wzoru na długość odcinak w układzie współrzędnych:
Długość odcinka w układzie współrzędnych jest równa odległości końców odcinka
![]()
i obliczamy ją ze wzoru:
U nas A=O=(0,0) i B=K=(6,8)
Mamy więc:
\( r=\sqrt{(6-0)^2+(8-0)^2}=\sqrt{36+64}=\sqrt{100}=10 \)
Stąd:
\( r^2=100 \)
Zaś równanie okręgu:
\( x^2+y^2=100 \)
Zatem:
 Odpowiedź
Odpowiedź
© medianauka.pl, 2023-01-04, ZAD-4601


Zadania podobne
Zadanie nr 2.
Napisać równanie okręgu, który został zilustrowany na poniższym rysunku.
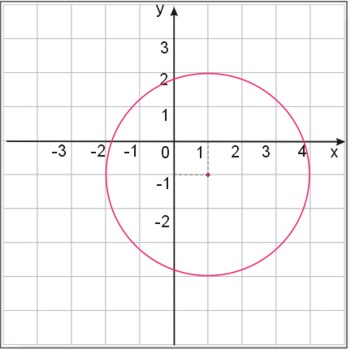
Zadanie nr 5.
Znaleźć równanie okręgu opisanego na trójkącie równobocznym, wyznaczonym przez punkty \(A=(1,1), B=(5,1), C=(3,2\sqrt{3}+1)\).
Zadanie nr 6.
Dany jest punkt \(A=(-1,1)\). Znaleźć punkt \(B\), jeżeli wiadomo, że \(|\vec{AB}|=4\).

Zadanie nr 7 — maturalne.
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych \(x\) i \(y\) takich, że \(x^2+y^2=2\), prawdziwa jest nierówność \(x+y\leq 2\).

Zadanie nr 8 — maturalne.
Liczba punktów wspólnych okręgu o równaniu \((x+2)^2+(y-3)^2=4\) z osiami układu współrzędnych jest równa:
A. 0
B. 1
C. 2
D. 4

Zadanie nr 9 — maturalne.
Dany jest okrąg o środku \(S=(2,3)\) i promieniu \(r=5\). Który z podanych punktów leży na tym okręgu?
A. \(A=(-1, 7)\)
B. \(B=(2, 3)\)
C. \(C=(3, 2)\)
D. \(D=(5, 3)\)

Zadanie nr 10 — maturalne.
Wyznacz równanie okręgu przechodzącego przez punkty \(A=(−5, 3)\) i \(B=(0, 6)\), którego środek leży na prostej o równaniu \(x−3y+1=0\).

Zadanie nr 11 — maturalne.
Dane są okręgi o równaniach \(x^2+y^2−12x−8y+43=0\) i \(x^2+y^2−2ax+4y+a^2−77=0\). Wyznacz wszystkie wartości parametru \(a\), dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.

