Zadanie maturalne nr 26, matura 2020
Treść zadania:
Rozwiąż nierówność \(2(x −1)(x + 3)>x −1\).
Rozwiązanie zadania
Rozwiązujemy nierówność:
\(2(x-1)(x+3)>x-1\)
\(2(x-1)(x+3)-(x-1)>0\)
\((x-1)[2(x+3)-1]>0\)
\((x-1)(2x+5)>0\)
\(2(x-1)(x+\frac{5}{2})>0/:2\)
\((x-1)(x+\frac{5}{2})>0\)
Mamy dwa pierwiastki \(x_=1, x_2=-\frac{5}{2}\), współczynnik a>0, więc rozpatrujemy wykres trzeci.
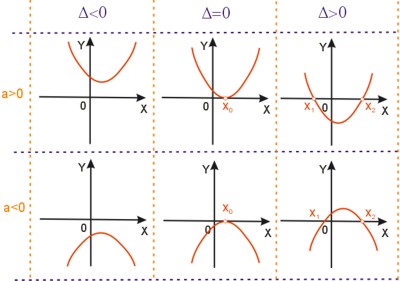
Szukamy wartości funkcji większych od zera. Stąd otrzymujemy rozwiązanie:
Odpowiedź
© medianauka.pl, 2023-03-04, ZAD-4757
Zadania podobne
Zadanie nr 1.
Dla jakiej wartości parametru \(x\) prawdziwa jest równość \(\sqrt{(x^2-2x+1)^2}=x^2-2x+1\)?
Zadanie nr 4.
Rozwiązać nierówność:
a) \(x^2+2x-3\geq 0\)
b) \(-x^2+\frac{3}{4}x-\frac{1}{8}> 0\)
c) \(-x^2+2\leq 0\)
Zadanie nr 5.
Rozwiązać nierówność:
a) \(\sqrt{3}x^2+\sqrt{2}x+1< 0\)
b) \(-x^2-2x-5\geq 0\)
Zadanie nr 6.
Rozwiązać nierówność:
a) \(x^2+8x+16> 0\)
b) \(-x^2+2\sqrt{2}x-2\geq 0\)
Zadanie nr 7.
Dla jakich wartości parametru \(m\) nierówność \(x^2-2x-m+1\leq 0\) ma jedno rozwiązanie \(x=1\)?
Zadanie nr 8.
Dla jakich wartości parametru \(m\) zbiorem rozwiązań nierówności \(x^2+mx-1+m> 0\) jest:
a) zbiór liczb rzeczywistych?
b) zbiór pusty?
